1 The manoeuvres of a surface ship may be seen
to take place in the xoyo-plane of a right-handed
system of axes Oo(xoyozo)
"fixed in space", the zo-axis of which is pointing downwards in the
direction of gravity. For the present discussion let the origin of
this system coincide with the position at time t = 0 of the midship
point O of the ship, and let the xo-axis be pointing in
the direction of ship’s heading at the same moment, the yo-axis
pointing to starboard. The future orientation of the ship in this
system is given by its heading angle ψ, its angle of pitch θ,
and its angle of roll ф (see figure
A1-1).
2 In calm conditions with no tide or current ship
speed through water (V) equals the speed over the ground, and the
progress along the ship track is equal to the time integral
3 This distance may conveniently be expressed
by the number of ship lengths sailed (i.e. by the non-dimensional
time):
4 In general the ship’s heading deviates
from the direction of the speed vector by the sideslip or drift angle
β. The advance and transfer parallel to and at right angles to
the original line of course (and ideal line of approach) are given
by the integrals:
5 Mathematical models of ship dynamics involve
expressions for the forces acting on the hull, usually separated in
their components along the axes of a system 0(xyz) moving with the
body. The full six-degrees-of-freedom motion of the ship may be defined
by the three components of linear velocities (u,v,w) along the body
axes, and by the three components of angular velocities (p,q,r) around
these axes. Again, for the present discussion it is sufficient to
consider the surface ship, moving with forward velocity a and sway
velocity v in the 0(xy) plane, and turning with yaw velocity r around
the z-axis normal to that plane. On these assumptions the speed V
= (u2+v2)1/2, the drift angle is
β = -tan-1(v/u) and the yaw rate is equal to the time
rate of change of heading angle ψ, i.e. r= -ψ=ψ. 
6 The non-dimensional yaw rate in terms of change
of heading (in radians) per ship length sailed is
which is also seen to be the non-dimensional measure
of the instantaneous curvature of the path of this ship L/R.
7 Many ships will experience a substantial rolling
velocity and roll angle during a turning manoeuvre, and it is understood
that the mathematical model used to predict the manoeuvring characteristics
should then include the more stringent expressions as appropriate.
8 Further information can be found in section
4.2 of the Standards for ship manoeuvrability.
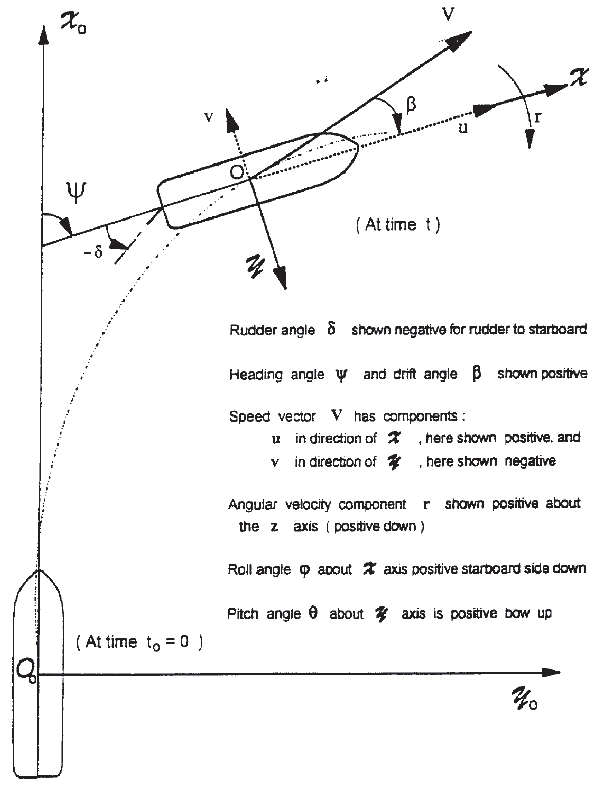
Figure A1-1 Surface ship with body axes O(xyz) manoeuvring within space-fixed
inertial frame with axes OO (xoyozo)