Section 1 Calculation procedure

1.1 The stress in individual plies of a laminate is calculated in accordance with Pt 8, Ch 3, Pt 8, Ch 3, 1 General of the Rules and Regulations for the Classification of Special Service Craft (hereinafter referred to as the Rules for Special Service Craft), based on bending moment (see Ch 3, 1 Calculation procedure 1.9) and the laminate stiffness of a 1 cm wide elemental strip of material.

1.2 Considering the model shown in Figure 3.1.1 Single skin example model and Figure 3.1.2 'Top-hat' stiffener used in model of a typical single skin hull laminate. Assume a pressure of 33 kN/m² and that there is no significant panel curvature.

Figure 3.1.1 Single skin example model

Figure 3.1.2 'Top-hat' stiffener used in model

1.3 In this example the maximum bending moment is determined from Pt 8, Ch 3, Pt 8, Ch 3, 1 General of the Rules for Special Service Craft and occurs under the web at the base of the stiffener. It should be noted that no reduction in the bending moment, M _b, due to aspect ratio effect is given since the panel aspect ratio, i.e. panel length/panel breadth is greater than 2. See Pt 8, Ch 3, Pt 8, Ch 3, 1 General of the Rules for Special Service Craft.

1.4 The laminate section modulus calculation is shown in Table 3.1.1 Tabulation of single skin laminiate calculations at the end of this Section. From Figure 3.1.3 Regions of tension (T) and compression (C) in example model it will be noted that there will be positions where tension and compression considerations will apply. Such calculations are ideally suited to computer based investigation.

Table 3.1.1 Tabulation of single skin laminiate calculations

	Ply No.	Discription	Gc	Weight	t	lever @	E	E.t	E.t.x	I @	EI @
				(g/m2)	(mm)	base, x (mm)	(N/mm2)			base	base
Dry see note	1	CSM	0,33	600	1,250	10,149	7200	9000	91341	1289,2	9281917
	2	CSM	0,33	600	1,250	8,899	7200	9000	80091	991,5	7139017
	3	CSM	0,33	600	1,250	7,649	7200	9000	68841	733,0	5277367
	4	CSM	0,33	600	1,250	6,399	7200	9000	57591	513,5	3696967
	5	WR	0,5	600	0,734	5,407	14000	10276	55562	214,9	3008869
	6	CSM	0,33	600	1,250	4,415	6950	8688	38355	245,3	1704699
	7	CSM	0,33	600	1,250	3,165	6950	8688	27496	126,8	881558
	8	WR	0,5	600	0,734	2,173	14500	10643	23127	35,0	507333
	9	CSM	0,33	600	1,250	1,181	6950	8688	10260	19,1	132482
	10	CSM	0,268	225	0,556	0,278	6290	3497	972	0,6	3604
Totals					10,774			86479	453637		31633812
Note 'Dry' indicates the inner surface or the hull and 'wet' the outside of the shell laminate

1.5 In order to apply a more detailed investigation it is necessary to establish the position of the neutral axis. However, in relatively balanced laminates this may be assumed to be at mid-depth. The procedure is simply to carry out the calculations assuming compressive properties on one face and tensile properties on the other face. Subsequently, the properties should be reversed and the layer stress calculations repeated. The calculated values should then be compared with the appropriate ultimate properties, i.e. dependent upon whether tension or compression considerations apply.

1.6 In the example the moments were evaluated about the base, which was taken to be the outer (wet) surface. The stiffness, EI, per 1 cm width, about the neutral axis, is determined using the parallel axis theorem:

In general:

where

1.7 A factor of 10 (width in mm) is introduced to correct the value of area used in the parallel axis theorem, since a 1 cm wide strip of material is considered in the calculations.

From the tabulation:

1.8 From Pt 8, Ch 3, Pt 8, Ch 3, 1 General of the Rules for Special Service Craft the individual layer stresses (tensile consideration) are determined from:

1.9 More generally, the calculation of the stresses in individual layers becomes:

where

1.10 Consider the following typical arrangement and the associated stresses for a single shell panel outside of the slamming zone:

Consider the outer (wet) surface:

Consider the 225g/m² chopped strand mat reinforcement in tension:

1.11 From Pt 8, Ch 3, Pt 8, Ch 3, 3.1 General 3.1.1 of the SSC Rules.

σ_{ult tension}= 82,2 N/mm² for CSM at G _c =0,286

Hence, stress fraction = 22,9/82,2 = 0,278.

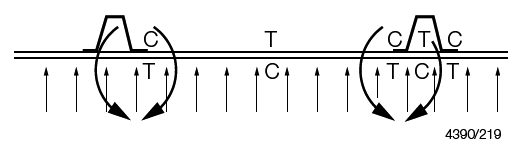
Figure 3.1.3 Regions of tension (T) and compression (C) in example model

1.12 From Table 7.3.1 Limiting stress criteria for local loading in Pt 8, Ch 7 of the Rules for Special Service Craft, the limiting tensile stress fraction is 0,33 for the side shell outside of the slamming zone. Hence, the calculated stress fraction is lower than the limiting stress factor and is therefore acceptable.

1.13 Similarly, consider the 600g/m² woven roving reinforcement in tension:

Stress fraction = 34,6/190 = 0,182

Hence acceptable.

1.14 Consider the inner (dry) surface:

The 600 g/m² chopped strand mat reinforcements at the inner surface in compression:

Stress fraction = 27,6/122 = 0,226

Hence acceptable.