
Section
3 Dished ends subject to internal pressure

3.1 Minimum thickness
3.1.1 The thickness, t, of semi-ellipsoidal and hemispherical unstayed ends, and
the knuckle section of torispherical ends, dished from plate, having
pressure on the concave side and satisfying the conditions listed
below, is to be determined by the following formula:
|
t
|
= |

|
t, p, D
o,
σ and J are as defined in Pt 5, Ch 9, 1.2 Definition of symbols

Figure 9.3.1 Shape factor
3.1.2 For semi-ellipsoidal
ends:
the external height, H ≥ 0,18D
o
D
o = the external diameter of the parallel
portion of the end, in mm
3.1.3 For torispherical
ends:
the internal radius, R
i ≤ D
o
the internal knuckle radius, r
i ≥
0,1D
o
the internal knuckle radius, r
i ≥ 3t
the external
height, H ≥ 0,18D
o, and is
determined as follows:

3.1.4 In addition
to the formula in Pt 5, Ch 9, 3.1 Minimum thickness 3.1.1 the thickness, t, of a torispherical head, made from more than one plate,
in the crown section is to be not less than that determined by the
following formula:
|
t
|
= |

|
t, p, R
i,
σ and J are as defined in Pt 5, Ch 9, 1.2 Definition of symbols.
3.1.8 The minimum
thickness permitted for vessels manufactured in corrosion resistant
steels will be the subject of special consideration.
3.1.9 For ends
which are butt welded to the drum shell, see
Pt 5, Ch 9, 1.9 Joint factors, the thickness of the edge of the
flange for connection to the shell is to be not less than the thickness
of an unpierced seamless or welded shell, whichever is applicable,
of the same diameter and material and determined by Pt 5, Ch 9, 2.1 Minimum thickness.

3.2 Shape factors for dished ends

3.3 Dished ends with unreinforced openings
3.3.1 Openings
in dished ends may be circular, obround or approximately elliptical.
3.3.2 The upper
curves in Figure 9.3.1 Shape factor provide
values of K to be used in Pt 5, Ch 9, 3.1 Minimum thickness 3.1.1, for ends with unreinforced openings. The selection of the
correct curve depends on the value  and a trial calculation is necessary to select the correct
curve, and a trial calculation is necessary to select the correct
curve,
|
d
|
= |
the
diameter of the largest opening in the end plate (in the case of an
elliptical opening, the larger axis of the ellipse), in mm |
|
t
|
= |
minimum
thickness, after dishing, in mm |
|
D
o
|
= |
outside diameter of dished end, in mm. |
3.3.3 The following
requirements must in any case be satisfied:

|
= |
≤ 0,10 |

|
= |
≤ 0,70 |

3.4 Flanged openings in dished ends
3.4.2 Where openings
are flanged, the radius, r
m, of the flanging
is to be not less than 25 mm, see
Figure 9.3.2 Typical dished ends(d). The thickness of the
flanged portion may be less than the calculated thickness.

3.5 Location of unreinforced and flanged openings in dished ends
3.5.1 Unreinforced
and flanged openings in dished ends are to be so arranged that the
distance from the edge of the hole to the outside edge of the plate
and the distance between openings are not less than those shown inFigure 9.3.3 Opening in dished ends.
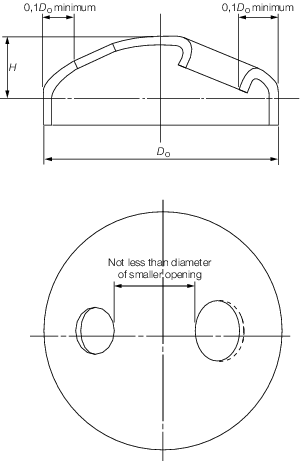
Figure 9.3.3 Opening in dished ends

3.6 Dished ends with reinforced openings
3.6.1 Where it
is desired to use a large opening in a dished end of less thickness
than would be required by Pt 5, Ch 9, 3.3 Dished ends with unreinforced openings,
the end is to be reinforced. This reinforcement may consist of a ring
or standpipe welded into the hole, or of reinforcing plates welded
to the outside and/or inside of the end in the vicinity of the hole,
or a combination of both methods, see
Figure 9.3.4 Limits of reinforcement. Forged reinforcements may
be used.
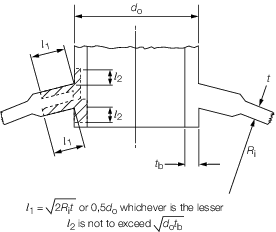
Figure 9.3.4 Limits of reinforcement
3.6.2 Reinforcing
material within the following limits may be taken as effective reinforcement:
-
The effective width l
1 of reinforcement is not to exceed or 0,5d
o, whichever is the lesser. or 0,5d
o, whichever is the lesser.
-
The effective length l
2 of a reinforcing ring is not to exceed
|
R
i
|
= |
the internal radius of the spherical part of a torispherical
end, in mm, or |
|
R
i
|
= |
the internal radius of the meridian of the ellipse at the centre
of the opening, of a semi-ellipsoidal end, in mm, and is given by
the following formula: |

|
d
o
|
= |
external diameter of ring or standpipe, in mm |
|
t
b
|
= |
actual thickness of ring or standpipe, in mm |
l1 and l2 are
as shown in Figure 9.3.4 Limits of reinforcement.
3.6.4 The area
shown in Figure 9.3.4 Limits of reinforcement is to be
obtained as follows:
- Calculate the cross-sectional area of reinforcement both inside
and outside the end plate within the length, l
1
- plus the full cross-sectional area of that part of the ring or
standpipe which projects inside the end plate up to the distance l
2
- plus the full cross-sectional area of that part of the ring or
standpipe which projects outside the internal surface of the end plate
up to a distance l
2, and deduct the sectional
area which the ring of standpipe would have if its thickness were
as calculated in accordance with Pt 5, Ch 9, 6.1 Minimum thickness.
3.6.5 If the
material of the ring or the reinforcing plates has an allowable stress
value lower than that of the end plate, then the effective cross-sectional
area, A, is to be multiplied by the ratio:


3.7 Torispherical dished ends with reinforced openings
3.7.1 If an opening
and its reinforcement are positioned entirely within the crown section,
the compensation requirements are to be as for a spherical shell,
using the crown radius as the spherical shell radius. Otherwise, the
requirements of Pt 5, Ch 9, 3.6 Dished ends with reinforced openings are to be applied.
|