Section 16 Longitudinal strength calculations
Clasification Society 2024 - Version 9.40
Clasifications Register Rules and Regulations - Rules and Regulations for the Classification of Ships, July 2022 - Part 4 Ship Structures (Ship Types) - Chapter 8 Container Ships - Section 16 Longitudinal strength calculations

Section 16 Longitudinal strength calculations

Parent topic: Chapter 8 Container Ships

16.1 Longitudinal extent of strength assessment

16.1.1 The stiffness, yield strength, buckling strength and hull girder strength assessment are to be carried out with due consideration given to locations where there are significant changes in the hull cross-section.

16.2 Symbols

16.2.1 The symbols used in this Section are defined as follows:
Cw = Waterplane coefficient at scantling draught T, to be taken as:
Cw = AW/(LB)
Aw = Waterplane area at scantling draught T, in m2
E = Modulus of elasticity, in N/mm2
Ms = Design still water bending moment, sagging (negative) and hogging (positive), in kNm
= Maximum permissible still water bending moment, sagging (negative) and hogging (positive), in kNm, to be taken negative or positive according to the convention given in Pt 3, Ch 4, 5.3 Design still water bending moments 5.3.2
Mw = Design hull vertical wave bending moment, sagging (negative) and hogging (positive), in kNm, to be taken negative or positive according to the convention given Pt 3, Ch 4, 5.3 Design still water bending moments 5.3.2
MU = Hull girder ultimate bending moment capacity, in kNm
Qs = Design hull still water shear force, in kN, to be taken as negative or positive according to the convention given in Pt 3, Ch 4, 6.4 Design still water shear force 6.4.2
= Permissible hull still water shear force, in kN.
Qw = Design hull wave shear force, in kN, to be taken as negative or positive according to the convention given in Pt 3, Ch 4, 6.4 Design still water shear force 6.4.2
qv = Shear flow along the cross-section under consideration
Inet = Net vertical hull girder moment of inertia at the cross-section under consideration, in m4, to be determined using net scantlings as defined in Table 8.16.3 Combination of still water and wave bending moments and shear forces
σHG = Hull girder bending stress, in N/mm2
τHG = Hull girder shear stress, in N/mm2
z = Vertical co-ordinate of location under consideration, in m
zn = Distance from baseline to the horizontal neutral axis, in m

16.3 Corrosion margin and net thickness

16.3.1 The strength is to be assessed using the net thickness approach for all scantlings.

16.3.2 The net thickness of the plates, webs and flanges is obtained as follows:
tnet = tas_built-tvol_add-αtc
Where:
tnet = Net thickness, in mm
tas_built = As built thickness, in mm
tvol_add = Voluntary addition, in mm
α = is given in Table 8.16.1 Values of corrosion addition factor

Table 8.16.1 Values of corrosion addition factor

Structural requirement Property/analysis type Corrosion addition factor, α
Strength assessment Section properties 0,5
Buckling strength Section properties (stress determination) 0,5
Buckling capacity 1,0
Hull girder ultimate strength Section properties 0,5
Buckling/collapse capacity 0,5

16.3.3 Where voluntary additions are to be applied, they are to be clearly indicated on the plans.

16.3.4 The total corrosion addition for both sides of a structural member is obtained as follows:
tc = (tc1+tc2) + tres

Where:

tc1 , tc2 re given in Pt 4, Ch 8, 16.3 Corrosion margin and net thickness 16.3.6
tres = reserve thickness, in mm, to be taken as 0,5 mm
16.3.5 For an internal member within a given compartment, the total corrosion addition is obtained as follows:
tc = (2tc1) + tres

16.3.6 The corrosion addition of a stiffener is to be determined based on the compartment in which it is located, see Pt 4, Ch 8, 16.3 Corrosion margin and net thickness 16.3.6

Table 8.16.2 Corrosion addition for one side of a structural member

Compartment type One side corrosion addition tc or tc2 in mm
Exposed to sea water 1,0
Exposed to atmosphere 1,0
Ballast water tank 1,0
Void and dry spaces 0,5
Fresh water, fuel oil and lube oil tank 0,5
Accommodation spaces 0,0
Container holds 1,0
Compartment types not mentioned above 0,5

16.3.7 The net section modulus, moment of inertia and shear area properties of a supporting member are to be calculated using the net dimension of the attached plate, web and flange as defined in Figure 8.16.1 Net sectional properties of supporting members

16.3.8 The net cross-sectional area, the moment of inertia about the axis parallel to the attached plate and the associated neutral axis are to be determined through applying a corrosion magnitude of deducted from the surface of the profile cross-section.

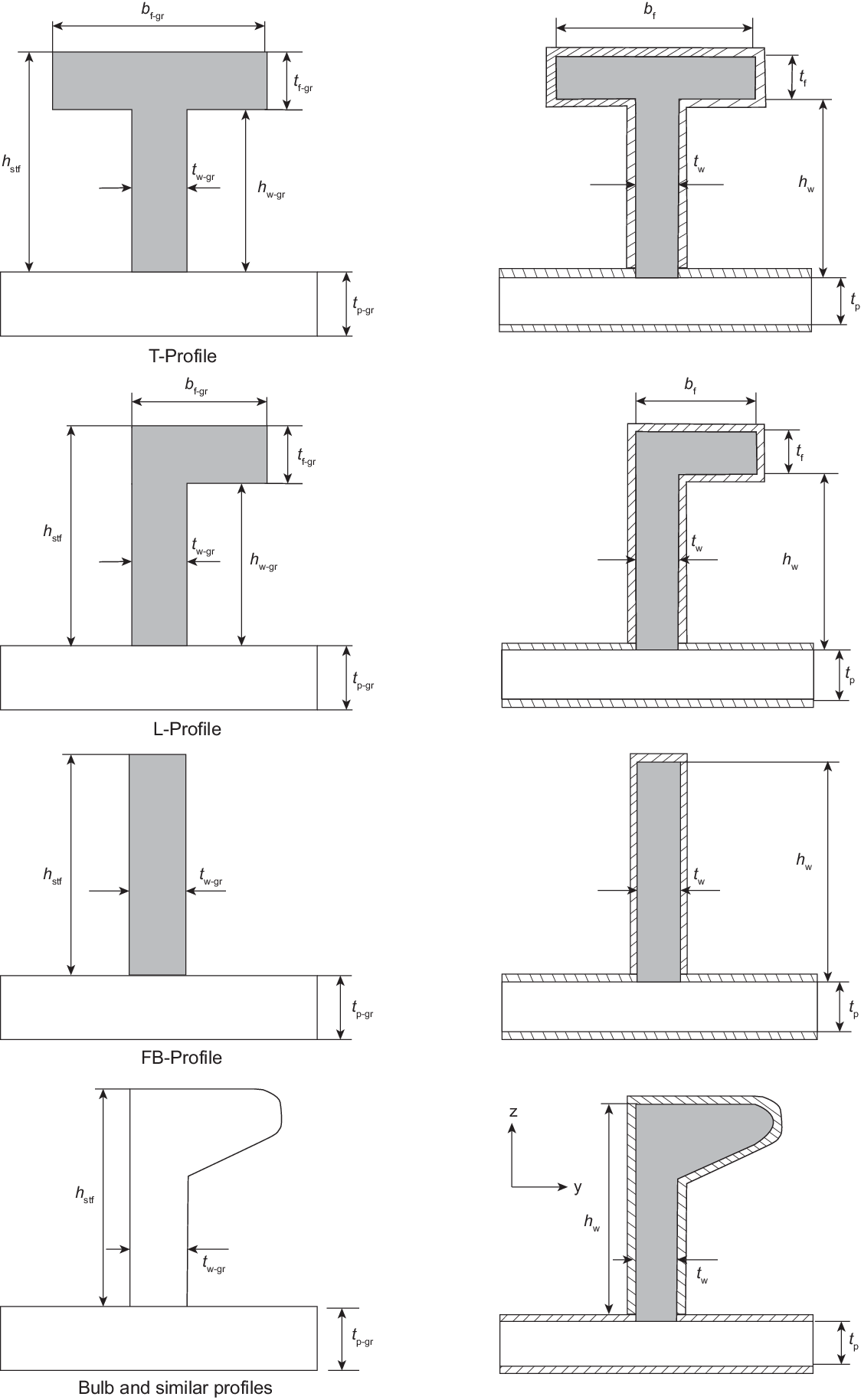
Figure 8.16.1 Net sectional properties of supporting members

16.4 Permissible still water bending moments and shear forces

16.4.1 The permissible still water bending moments, Ms in kNm, and still water shear forces, Qs in kNm, are to be calculated at each section along the ship’s length for design loading conditions as specified in Pt 3, Ch 4, 5.3 Design still water bending moments.

16.5 Hull moment of inertia

16.5.1 The hull section moment of inertia about the transverse neutral axis, at any position along the ship, is to be not less than the following for both hogging and sagging cases (see also Table 8.16.3 Combination of still water and wave bending moments and shear forces):

16.6 Design vertical wave bending moments

16.6.1 The appropriate hogging or sagging design hull vertical wave bending moment, at any position along the ship, may be taken as follows:
Mw =

Where:

f1 is the ship service factor, to be taken as 0,85

CW and C3 are given in Pt 4, Ch 8, 16.2 Symbols 16.2.1 and Pt 4, Ch 8, 16.6 Design vertical wave bending moments 16.6.2 respectively

f2 is the hogging,ffH , or the sagging, ffS correction factor

ffH is the hogging (positive) moment correction factor and is to be taken as:
ffH = not to be taken greater than 1,1
ffS is the sagging (negative) moment correction factor and is to be taken as:
ffS = , not to be taken less than 1,0

fbow and Kf are given in Pt 4, Ch 8, 16.6 Design vertical wave bending moments 16.6.3 and Pt 4, Ch 8, 16.6 Design vertical wave bending moments 16.6.4 respectively

Kf is given in Pt 4, Ch 8, 16.6 Design vertical wave bending moments 16.6.4

B and L are given in Pt 4, Ch 8, 1.5 Symbols and definitions

16.6.2 The wave parameter, C3, is to be taken as:
C3 =
C3 =
Where:
L4 =
16.6.3 The bow flare shape, fbow coefficient is to be taken as:
fbow =
Where:
  • ADK is the projected area in the horizontal plane of the uppermost deck, in m2, including the forecastle deck, if any, forward of 0,8L from the AP, see also Figure 8.16.2 Projected area ADK and vertical distance zf. Any other structures, e.g. plated bulwark, are to be excluded.
  • AWLis the waterplane area, in m2, at draught T, forward of 0,8L from the AP
  • zf is the vertical distance, in m, from the waterline at draught T, to the uppermost deck at side (or forecastle deck), measured at the FP, see also Figure 8.16.2 Projected area ADK and vertical distance zf. Any other structures, e.g. plated bulwark, are to be excluded.

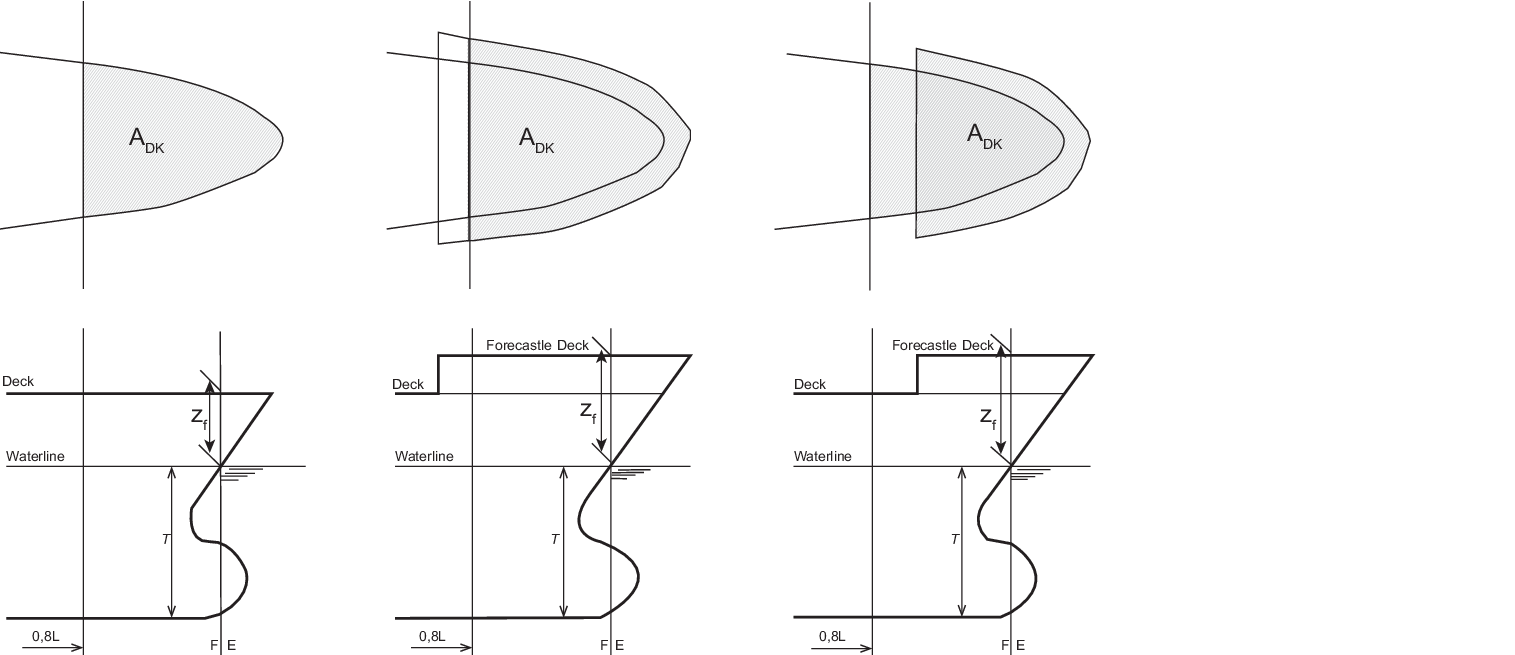
Figure 8.16.2 Projected area ADK and vertical distance zf

16.6.4 The distribution of the vertical wave bending moment, Kf , is to be taken as:
  1. Hogging (positive) moments, see also Figure 8.16.3 Distribution of vertical wave bending moment Mw along the ship length
    Kf = 0 at aft end of L
    = 0,15 at 0,1 L
    = 1,0 between 0,35 L and 0,55 L
    = 0,25 at 0,8 L
    = 0 at forward end of L
  2. Sagging (negative) moments, see also Fig 8.16.3
    Kf = 0 at aft end of L
    = -1,0 between 0,35 L and 0,6 L
    = 0 at forward end of L
Intermediate values are to be obtained by linear interpolation.

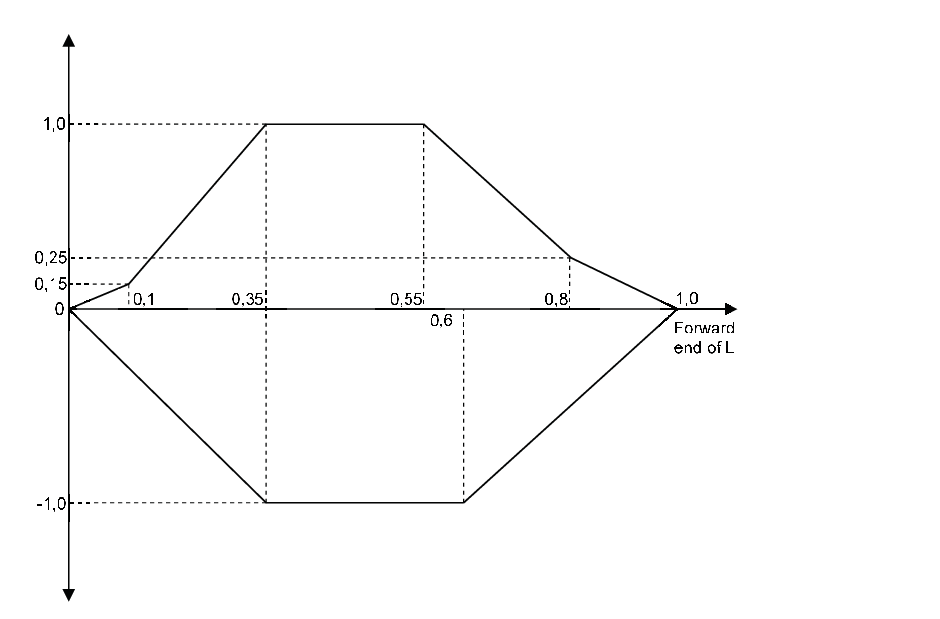
Figure 8.16.3 Distribution of vertical wave bending moment Mw along the ship length

16.7 Design vertical wave shear force

16.7.1 The design hull wave shear force,Qw , at any position along the ship is to be taken as:
Qw =
Where:
f1 = ship service factor, to be taken as 0,85

Cw, C3 and Kf are defined in Pt 4, Ch 8, 16.2 Symbols, Pt 4, Ch 8, 16.7 Design vertical wave shear force 16.7.2 and Pt 4, Ch 8, 16.7 Design vertical wave shear force 16.7.3 respectively B and L are given in Pt 4, Ch 8, 1.5 Symbols and definitions 1.5.1

16.7.2 The wave parameter, C3, is to be taken as:
C3 =
C3 =
Where:
L4 =
16.7.3 The distribution of the wave shear force, Kf , is to be taken as follows, see also Figure 8.16.4 Distribution of vertical shear force Qw along the ship length.
  1. Positive shear force
    Kf = 0 at aft end of L
    Kf = 5,2(0,3 + 0,7 ffH) between 0,2 L and 0,3 L
    Kf = 4,0 between 0,4 L and 0,55 L
    Kf = 5,7 (0,25 + 0,75 ffS) between 0,65 L and 0,85 L
    Kf = 0 at forward end of L
  2. Negative shear force
    Kf = –1,3(0,3 + 0,7 ffS) at aft end of L
    Kf = –5,2(0,3 + 0,7 ffS) between 0,15 L and 0,3 L
    Kf = -4,0 between 0,4 L and 0,5 L
    Kf = -5,7 ffH between 0,6 L and 0,75 L
    Kf = 0 at forward end of L

Intermediate values of Kf to be obtained by linear interpolation.

ffH and ffS are as defined in Pt 4, Ch 8, 16.6 Design vertical wave bending moments 16.6.1.

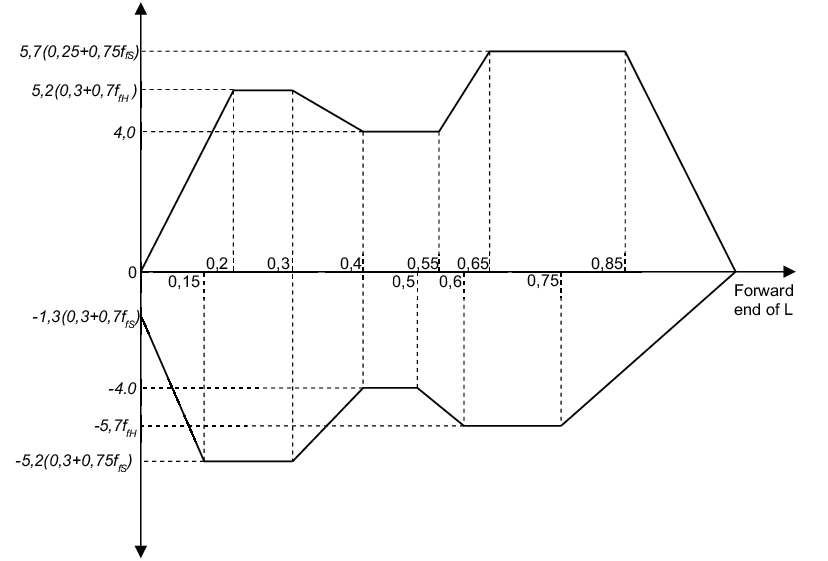
Figure 8.16.4 Distribution of vertical shear force Qw along the ship length

16.8 Permissible hull girder stresses

16.8.1 The permissible combined (still water plus wave) stress for hull vertical bending, σ , is given by:
σ =
16.8.2 The permissible shear stress, τ , is given by:
τ =

16.9 Hull girder stresses

16.9.1 The hull girder bending stresses, σG, in N/mm2 are to be determined for the section under consideration for the load cases given in Table 8.16.3 Combination of still water and wave bending moments and shear forces at the following locations:
  1. At bottom.
  2. At deck.
  3. At top of hatch coaming.
  4. At any point where there is a change of steel yield strength.
σG =

Where:

Mw and Ms are defined in Table 8.16.3 Combination of still water and wave bending moments and shear forces.

γs, γw are partial safety factors to be taken as:
γs = 1,0
γw = 1,0
And:
16.9.2 The hull girder shear stresses, τG , in N/mm2 are to be determined for the section under consideration for the load cases given in Table 8.16.3 Combination of still water and wave bending moments and shear forces for all structural elements which contribute to the shear strength capability of the ship.
τG =

Where:

Qw and Qs are defined in Table 8.16.3 Combination of still water and wave bending moments and shear forces.

γs, γw are partial safety factors to be taken as:
γs = 1,0
γw = 1,0
  • qv is calculated in accordance with the ShipRight Procedure Additional calculation procedures for longitundinal strength
And:

Table 8.16.3 Combination of still water and wave bending moments and shear forces

Load case Bending moment Shear force
Still water, Ms Wave, Mw Location, x Still water, Qs Wave, Qw
Hogging M smax M wmax Qsmax Qwmax
Qsmin Qwmin
Sagging M smin M wmin Qsmin Qwmin
Qsmax Qwmax
Symbols
Msmax = positive still water bending moment at the cross-section under consideration
Msmin = negative still water bending moment at the cross-section under consideration
Mwmax = wave bending moment at the cross-section under consideration, to be taken as the positive value of Mw as defined in Pt 4, Ch 8, 16.6 Design vertical wave bending moments 16.6.1
Mwmin = wave bending moment at the cross-section under consideration, to be taken as the negative value of Mw as defined in Pt 4, Ch 8, 16.6 Design vertical wave bending moments 16.6.1
Qsmax = positive still water shear force at the cross-section under consideration
Qsmin = negative still water shear force at the cross-section under consideration taken as
Qwmax = maximum value of the wave shear force at the cross-section under consideration, to be taken as the positive value of Qw as defined in Pt 4, Ch 8, 16.7 Design vertical wave shear force 16.7.1
Qwmin = minimum value of the wave shear force at the cross-section under consideration, to be taken as the negative value of Qw as defined in Pt 4, Ch 8, 16.7 Design vertical wave shear force 16.7.1
x = longitudinal coordinate or a location under consideration
16.9.3 The hull girder stresses for the two load cases (hogging and sagging) defined in Pt 4, Ch 8, 16.9 Hull girder stresses 16.9.1 and Pt 4, Ch 8, 16.9 Hull girder stresses 16.9.2 are to meet the following criteria:

16.10 Buckling strength assessment

16.10.1 The following requirements apply to plate panels and longitudinal stiffeners subject to hull girder bending and shear stresses.

16.10.2 The acceptance criteria for the buckling assessment are defined as follows:
  • ηact ≤ 1
Where:
  • ηact is the maximum utilisation factor
16.10.3 The utilisation factor, ηact, is given by:
ηact =
Where:
16.10.4 Failure state limits are defined in ShipRight Procedure Additional calculation procedures for longitudinal strength for the following items:
  1. Elementary plate panels
  2. Overall stiffened panels
  3. Longitudinal stiffeners

Each failure limit state is defined by an equation and, γc, is to be determined such that it satisfies the equation.

16.10.5 The stress multiplication factor at failure, γc, of a structural member is to be determined for any combination of longitudinal and shear stress, see Figure 8.16.5 Example of failure state limit curve and stress multiplication factor at failure.

Where:
  • σx τx is the applied stress combination for buckling given in Pt 4, Ch 8, 16.10 Buckling strength assessment
  • σc τc is the critical buckling stress obtained in accordance with the ShipRight Procedure Additional calculation procedures for longitudinal strength for the stress combination for buckling σ and τ

Figure 8.16.5 Example of failure state limit curve and stress multiplication factor at failure

16.10.6 The following two stress combinations are to be considered for each of the load cases defined in Pt 4, Ch 8, 16.9 Hull girder stresses 16.9.1. The stresses are to be derived at the load calculation points defined in Pt 4, Ch 8, 16.10 Buckling strength assessment 16.10.7 and Pt 4, Ch 8, 16.10 Buckling strength assessment 16.10.8
  1. Longitudinal framing
    Stress combination 1 with:
    σx = σHG
    σy = 0
    τ = 0,7 τHG
    Stress combination 2 with:
    σx = 0,7 σHG
    σy = 0
    τ = τHG
  2. Transverse framing
    Stress combination 1 with:
    σx = 0
    σy = σHG
    τ = 0,7 τHG
    Stress combination 2 with:
    σx = 0
    σy = 0,7 σHG
    τ = τHG

16.10.7 The hull girder stresses for elementary plate panels are to be calculated at the load calculation points defined in Pt 4, Ch 8, 16.10 Buckling strength assessment 16.10.8.

16.10.8 The hull girder stresses for longitudinal stiffeners are to be calculated at the following load calculation points:
  1. At the mid length of the stiffener under consideration
  2. At the intersection point between the stiffener and its attached plate

Table 8.16.4 Load calculation points (LCP) for plate buckling assessment

LCP coordinates Hull girder bending stress Hull girder shear stress
x coordinate Mid length of the elementary plate panel (EPP)
y coordinate Both upper and lower ends of the EPP, points A1 and A2 in Figure 8.16. Mid-point of EPP, point B in Figure 8.16.
z coordinate Distance from baseline to load calculation point

Figure 8.16.6 Load calculation points for plate buckling

16.11 Hull girder ultimate strength

16.11.1 The hull girder ultimate strength assessment is to be carried out for ships with a length L greater than or equal to 150 m.

16.11.2 The acceptance criteria given in Pt 4, Ch 8, 16.11 Hull girder ultimate strength 16.11.8, are applicable to intact ships only.

16.11.3 The hull girder ultimate bending capacity,MU , is defined as the maximum bending moment capacity of the hull girder beyond which the hull structure collapses.

16.11.4 The hull girder ultimate bending capacity is to be checked for the load cases defined in Table 8.16.3 Combination of still water and wave bending moments and shear forces.

16.11.5 The ultimate bending moment capacities of a hull girder transverse section, in hogging and sagging conditions, are defined as the maximum values of the curve of bending moment M versus the curvature Χ of the transverse section considered

where:

16.11.6 The hull girder ultimate bending capacity, MU, is to be calculated using the incremental-iterative method as given in Chapter 4 of ShipRight Procedure Additional calculation procedures for longitudinal strength.

16.11.7 The vertical hull girder bending moment, M in hogging and sagging conditions, to be considered in the ultimate strength check is to be taken as:
M = γs Ms + γw Mw
Where:
Ms = permissible still water bending moment, in kNm, as defined in Pt 4, Ch 8, 16.4 Permissible still water bending moments and shear forces 16.4.1
Mw = vertical wave bending moment, in kNm, as defined in Pt 4, Ch 8, 16.6 Design vertical wave bending moments 16.6.1
γs = partial safety factor for the still water bending moment, to be taken as 1,0
γw = partial safety factor for the vertical wave bending moment, to be taken as 1,2
16.11.8 The hull girder ultimate bending capacity at any hull transverse section is to satisfy the following criteria:
Where:
M = vertical bending moment, in kNm, as defined in Pt 4, Ch 8, 16.11 Hull girder ultimate strength 16.11.7
MU = hull girder ultimate bending moment capacity, in kNm, as defined in Pt 4, Ch 8, 16.11 Hull girder ultimate strength 16.11.6
γM = partial safety factor covering material, geometric and strength prediction uncertainties, to be taken as 1,05
γDB = partial safety factor covering the effect of double bottom bending, to be taken as:
γDB = 1,15 for hogging condition
γDB = 1,0 for sagging condition
  • For cross-sections where the double bottom breadth of the inner bottom is less than that at amidships or where the double bottom structure differs from that at amidships (e.g. engine room sections), the factor, γDB, for the hogging condition may be specially considered.

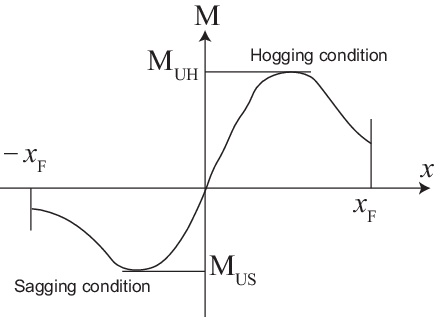
Figure 8.16.7 Bending moment M versus curvature Χ
Copyright 2022 Clasifications Register Group Limited, International Maritime Organization, International Labour Organization or Maritime and Coastguard Agency. All rights reserved. Clasifications Register Group Limited, its affiliates and subsidiaries and their respective officers, employees or agents are, individually and collectively, referred to in this clause as 'Clasifications Register'. Clasifications Register assumes no responsibility and shall not be liable to any person for any loss, damage or expense caused by reliance on the information or advice in this document or howsoever provided, unless that person has signed a contract with the relevant Clasifications Register entity for the provision of this information or advice and in that case any responsibility or liability is exclusively on the terms and conditions set out in that contract.