Section 5 Design load systems for structural components or longitudinally ineffective material
Clasification Society 2024 - Version 9.40
Clasifications Register Rules and Regulations - Rules and Regulations for the Classification of Naval Ships, January 2023 - Volume 1 Ship Structures - Part 7 Enhanced Structural Assessment (Provisional) - Chapter 2 Total Design Loads - Section 5 Design load systems for structural components or longitudinally ineffective material

Section 5 Design load systems for structural components or longitudinally ineffective material

Parent topic: Chapter 2 Total Design Loads

5.1 Deck structures (DK)

5.1.1 The design pressure, P WD, for weather deck structure is given in Vol 1, Pt 7, Ch 2, 3.6 External shell pressures 3.6.2.

5.1.2 For weather decks and interior decks subjected to cargo loads or other pressure loading then the following design pressure is to be used for the plating and stiffeners if it is greater than that given in Vol 1, Pt 7, Ch 2, 5.1 Deck structures (DK) 5.1.1:

P CD = wf W cd kN/m2

where

W cd is the static pressure exerted by the cargo, payload, stores or equipment on the deck as specified by the designer in kN/m2, see Vol 1, Pt 7, Ch 2, 2.1 Nomenclature 2.1.2 and see also Vol 1, Pt 5, Ch 3, 5.4 Loads for decks designed for cargo or heavy equipment loads, Pcd and Wcd 5.4.1

w f is given in Vol 1, Pt 7, Ch 2, 3.5 Inertial force load combination factor, wf 3.5.1

5.1.3 The design pressure, , for interior deck plating and stiffeners is given by:

= w f W in kN/m2

is not to be taken less than 2,5 kN/m2

W in is defined in Vol 1, Pt 7, Ch 2, 2.1 Nomenclature 2.1.2

5.1.4 For weather or internal decks which form part of a deep tank or watertight boundary then the pressure loading is to be taken as the greater of the following if this is greater than the above:

P tk = 9,81ρ (H tk – z) kN/m2 (deep tank, if applicable)
P da = 10(H da – z) kN/m2 (WT subdivision, only if applicable and for loading conditions which represent damaged situations)

where

ρ = specific density of liquid in the tank, to be taken as not less than 1,025
z = distance above the baseline of the mid depth of the deck plating

H tk and H da are defined in Vol 1, Pt 7, Ch 2, 2.1 Nomenclature 2.1.2

5.1.5 The cargo deck design force matrix, [F CD], for plating and stiffeners is to be taken as below for all mass items which act over the deck area considered

  1. [F CD] = w f [W ma]

W ma is the weight of each item on the deck as specified by the designer in kN. See also Vol 1, Pt 5, Ch 3, 5.4 Loads for decks designed for cargo or heavy equipment loads, Pcd and Wcd 5.4.2

5.1.6 If the deck is required to be immersed during its operation, e.g. an internal dock area, then the deck is to be designed using the side shell pressure loads, P SS, see Vol 1, Pt 7, Ch 2, 3.6 External shell pressures 3.6.1

5.2 Transverse watertight and deep tank bulkheads (BH)

5.2.1 The design normal pressure for bulkhead plating, P BHP, and stiffeners, P BHS, is to be taken as the pressure values P bhp and P bhs respectively given in Vol 1, Pt 5, Ch 3, 5.8 Design pressures for watertight and deep tank bulkheads and boundaries

5.2.2 The design impulse pressure, P BH, for the bulkhead plating and stiffeners may be ignored, unless these members are likely to be subjected to significant sloshing loads or similar.

5.2.3 The design transverse load, LT BH, due to hydrostatic and hydrodynamic compressive loading is to be taken as follows:

LT BH = –εBH P SS H bh S bh kN

where

H bh = half the vertical distance from the deck below the bulkhead under consideration to the deck above, in metres, see Figure 2.5.1 Design parameter H bh for transverse loads and Figure 2.5.2 Design loads for bulkheads
S bh = half the longitudinal distance between adjacent transverse bulkheads, in metres
εBH = effectiveness of the bulkhead, i.e. the relative proportion of the load carried by the bulkhead as opposed to other structure such as decks

εBH may be taken as 0,5

alternatively εBH may be taken as

εBH = H bh/(2S bh) for H bh < S bh
and = 1 – S bh/(2H bh) for H bh > S bh

P SS is to be taken at the mid height of the H bh depth, P SS is defined in Vol 1, Pt 7, Ch 2, 3.6 External shell pressures 3.6.1

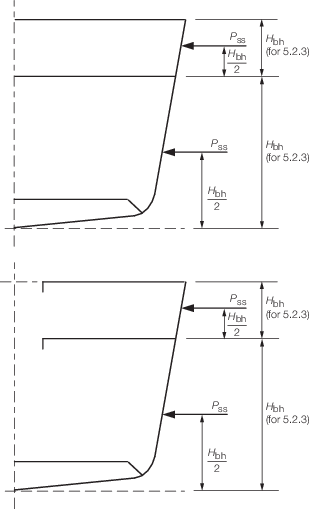
Figure 2.5.1 Design parameter H bh for transverse loads

5.2.4 The design vertical load, LV BH, supported by the transverse bulkheads is to be based on the pressure loads acting on the plating of the supported deck over, P CD, the local inertial forces, [F CD], and the bulkhead loads above, L A. The design vertical load is to be taken as

LV BH = –(B bh S bh P CD + [F CD] + L A) kN

where

B bh = breadth of the deck supported by the bulkhead, in metres
L A = load, in kN, the bulkhead above, assumed zero if there are is over, see Vol 1, Pt 7, Ch 2, 4.2 Side shell structures (SS) 4.2.5
F CD = inertial load or loads, in kN, from items of equipment, etc. on the supported deck, assumed zero if there is none over. F CD is defined in Vol 1, Pt 7, Ch 2, 5.1 Deck structures (DK) 5.1.5

P CD is defined in Vol 1, Pt 7, Ch 2, 5.1 Deck structures (DK) 5.1.2

5.2.5 Normally, the design shear force, QVBH, may be ignored for bulkhead plating. However, if the structural arrangement or load paths are such that significant shear load is carried by the bulkhead, then it should be considered, e.g. when the bulkhead is not continued down to the bottom shell. In this case the design shear force, acting in the vertical direction, is to be taken as

QVBH = LV BH /2 kN

where

LV BH is given in Vol 1, Pt 7, Ch 2, 5.2 Transverse watertight and deep tank bulkheads (BH) 5.2.4

Figure 2.5.2 Design loads for bulkheads

5.3 Deckhouses, bulwarks and superstructures (DH)

5.3.1 The design normal pressure, P DH, for the plating and stiffeners of deckhouses, bulwarks and the first tier and above of superstructures is given by:

P DH = P dh kN/m2

5.3.2 For the side plating and longitudinal bulkheads of deckhouses and superstructures, the design vertical load, LV DH, at each intersecting deck level is to be taken as follows: LV DH = –εDH (S dh B dh P CD + L A + [F CD]) kN

where

P CD = basic deck design pressure, as appropriate, plus any other local loadings directly above the pillar, in kN/m2
[F CD] = inertial load or loads, in kN, from items of equipment, etc. on the supported deck, assumed zero if there is none over. F CD is defined in Vol 1, Pt 7, Ch 2, 5.1 Deck structures (DK) 5.1.5
L A = appropriate portion of the load or loads, in kN, from pillar(s) or bulkhead(s) above, assumed zero if there is none over, see Vol 1, Pt 7, Ch 2, 4.2 Side shell structures (SS) 4.2.5
εDH = effectiveness of the side plating or longitudinal bulkhead, i.e. the relative proportion of the load carried by this plating as opposed to other structure such as the transverse bulkheads
= 0,5

S dh B dh is the effective deck area supported by the deckhouse side plating or longitudinal bulkheads and can be taken as follows:

B dh = mean spacing of longitudinal bulkheads, side shell or effectively supported longitudinal girders, in metres.
S dh = span or length of the side plating or longitudinal bulkhead between major deckhouse transverse bulkheads, in metres.

5.3.3 For transverse bulkheads of deckhouses and superstructures, the design vertical load, LV DH, at each intersecting deck level is to be taken as follows:

LV DH = –εDH (S dh B dh P CD + L A + [F CD]) kN

where

εDH = efficiency of the transverse bulkheads i.e. the relative proportion of the load carried by the transverse bulkheads as opposed to other structure such as the side plating
= 0,5

S dh B dh is the effective deck area supported by the transverse bulkhead and can be taken as follows:

S dh = mean spacing of transverse bulkheads, in metres.
B dh = breadth of the transverse bulkhead, in metres.

5.3.4 For decks of deckhouses, the design transverse load, LT DH, at each deck level may normally be ignored.

5.3.5 If the superstructure or deckhouse is longitudinally effective then the design global vertical bending moment and shear force are to be taken as M D and Q D respectively, see Vol 1, Pt 7, Ch 2, 3.3 Design global loads – Intact conditions or Vol 1, Pt 7, Ch 2, 3.4 Design global loads – Damaged conditions or Residual Strength Assessment (RSA) conditions for the design of the side plating and longitudinal bulkheads of deckhouse structures.

5.4 Transverse floors (FL)

5.4.1 The design normal pressure, P FL, for the web plating of floors of double bottom or single bottom structures is to be taken as the greater of the following:

  1. P tk kN/m2 (Deep tank floor).

  2. P da kN/m2 (WT subdivision, only if applicable and for loading conditions which represent damaged situations).

  3. 5 kN/m2 (minimum value).

where

P da and P tk are defined inVol 1, Pt 7, Ch 2, 5.1 Deck structures (DK) 5.1.4

5.4.2 The design impulse pressure, P FL, for the web plating of floors may be ignored, unless these members are subjected to sloshing loads or similar.

5.4.3 The design vertical load, LV FL, for the floors is to be based on the pressure loads acting on the plating of the inner bottom P CD (downwards) and the bottom shell P BS (upwards), the local inertial forces [F CD] and pillar bulkhead loads above L A. The design vertical load, LV FL, is to be taken as:

LV FL = –εFLV ( (P CD – P BS) + [F CD] + L A) kN

where

εFLV = effectiveness of the floors in the vertical direction, i.e. the relative proportion of the load carried by the transverse floors as opposed to bottom girders, etc.
= 1,0 for the floor halfway between transverse bulkheads
= mean spacing of transverse floors, in metres, see Figure 2.5.3 Loads to be applied to transverse floors
L A = load, in kN, from pillar(s) or bulkhead(s) above, assumed zero if there is none over, see Vol 1, Pt 7, Ch 2, 4.2 Side shell structures (SS) 4.2.5
F CD = inertial load or loads, in kN, from items of equipment, etc. on the supported deck, assumed zero if there is none over. F CD is defined in Vol 1, Pt 7, Ch 2, 5.1 Deck structures (DK) 5.1.5
= breadth of the transverse floor between longitudinal bulkheads or side shell(s), in metres. NOTE may be full breadth

P BS is defined in Vol 1, Pt 7, Ch 2, 4.1 Bottom shell structures (BS) 4.1.2

P CD is defined in Vol 1, Pt 7, Ch 2, 5.1 Deck structures (DK) 5.1.2

Note
  • For single bottom floors P CD is likely to be zero.
  • It may be necessary to take account of the impact loading on the bottom plating in the derivation of LVFL and QVFL.

5.4.4 The design transverse load, LT FL, for the floor plating due to hydrostatic and hydrodynamic compressive loading is to be taken as follows:

LT FL = –εFLT P SS H d kN

where

εFLT = effectiveness of the floors in the transverse direction, i.e. the relative proportion of the load carried by the floor plating as opposed to other bottom structure
= 0,3f b for double bottom structures
= 0,5f b for single bottom structures
f b = 2,0 for bottom structures where transverse elastic buckling of outer bottom plating is likely
= 3,0 for bottom structures where transverse elastic buckling of inner and outer bottom plating is likely
= 1,0 otherwise

P SS and H d are to be taken as the values defined for the bottom structure in Vol 1, Pt 7, Ch 2, 4.1 Bottom shell structures (BS) 4.1.5

5.4.5 The design shear force, QVFL, for the floor web plating due to local loading acts in the vertical direction and is to be taken as:

QVFL = εFLV ( (P CD – P BS) + [F CD] + L A)/2 kN

5.4.6 The design bending load for bottom floor primary member is to be taken as LV FL.

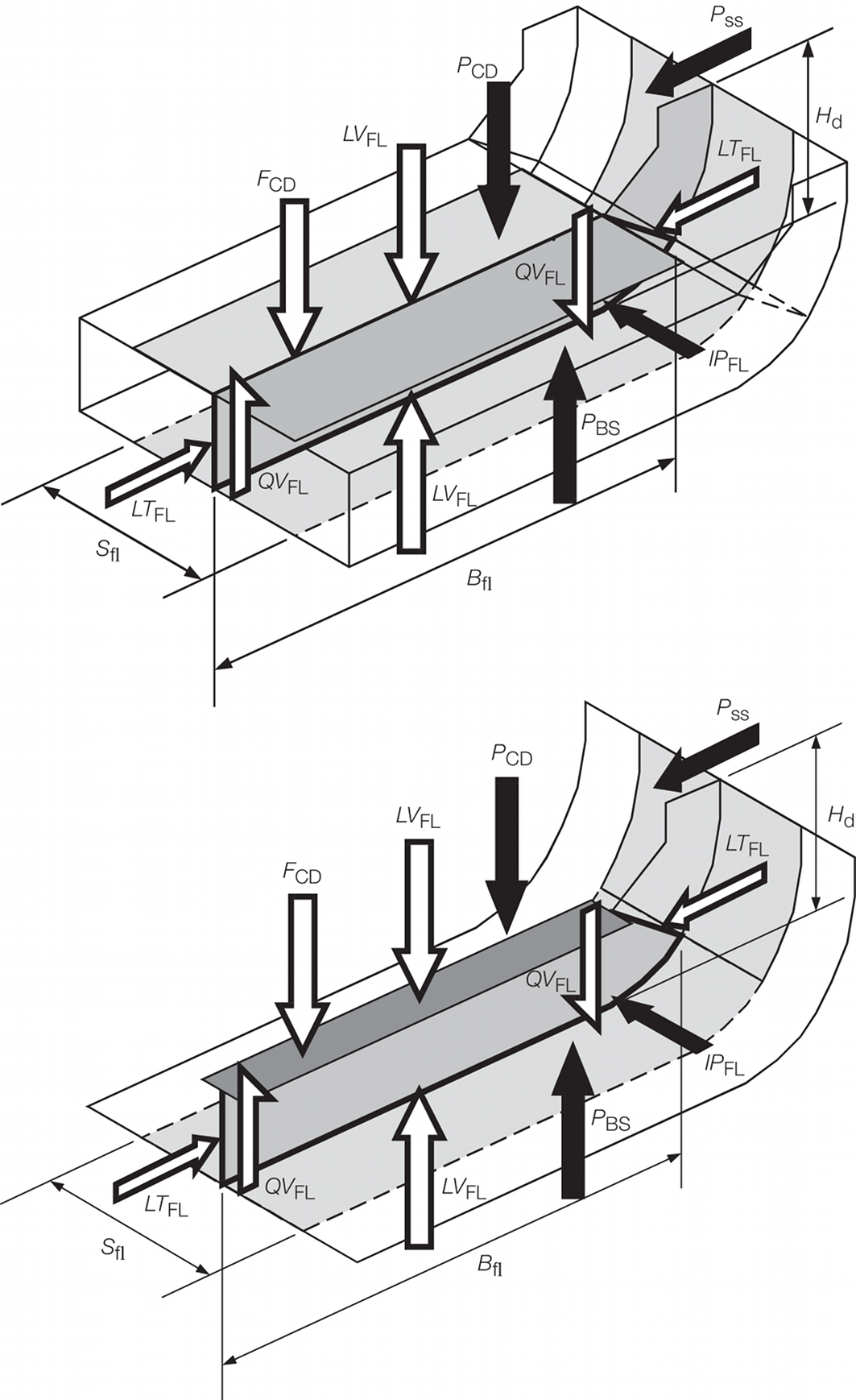
Figure 2.5.3 Loads to be applied to transverse floors

5.4.7 The membrane loads acting on the bottom shell plating are defined in Vol 1, Pt 7, Ch 2, 4.1 Bottom shell structures (BS). The membrane loads acting on the inner bottom plating are defined in Vol 1, Pt 7, Ch 2, 4.4 Inner bottom structures (IB) These membrane loads are required to assess the transverse floors in addition to the local bending loads.

5.5 Side frames and web frames (SF)

5.5.1 This sub-Section covers side frames, web frames and frames supporting longitudinal bulkheads.

5.5.2 The design normal pressure, P SF, for the web plating of side frames may be ignored.

5.5.3 The design impulse pressure, P SF, for the web plating of side frames may be ignored, unless these members are subjected to sloshing loads or similar.

5.5.4 The design vertical load, LV SF, for the side frames, including the attached plating, is to be based on the pressure loads acting on the plating of the supported deck over, P CD, the local inertial forces, [F CD], and side frame loads above, L A. The design vertical load is to be taken as:

LVSF = – (B fr S fr P CD + [F CD] + L A) kN

where

S fr = mean spacing of side frames, in metres, see Figure 2.5.4 Loads to be applied to side frames
B fr = breadth of the deck supported by the side frame, in metres
L A = load, in kN, the side frame above, assumed zero if there is none over, see Vol 1, Pt 7, Ch 2, 4.2 Side shell structures (SS) 4.2.5
F CD = inertial load or loads, in kN, from items of equipment, etc. on the supported deck, assumed zero if there is none over. F CD is defined in Vol 1, Pt 7, Ch 2, 5.1 Deck structures (DK) 5.1.5

P CD is defined in Vol 1, Pt 7, Ch 2, 5.1 Deck structures (DK) 5.1.2

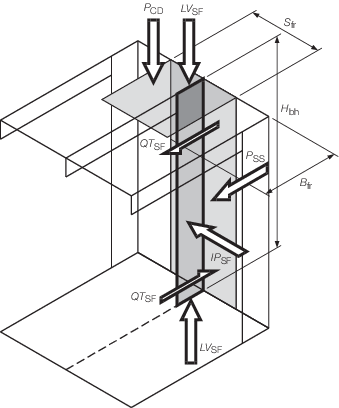
Figure 2.5.4 Loads to be applied to side frames

5.5.5 The design transverse load, LT SF, may be ignored for the side frames.

5.5.6 The design shear force, QT SF, for the side frame web plating due to local loading acts in the transverse direction and is to be taken as:

QT SF = H fr S fr P SS/2 kN

where

H fr = length of the side frame between adjacent decks, see Figure 2.5.4 Loads to be applied to side frames

P SS is to be taken at the mid height of the side frame, P SS is defined in Vol 1, Pt 7, Ch 2, 3.6 External shell pressures 3.6.1

NOTE

It may be necessary to take account of the impact loading on the side frame plating in the derivation of QT SF.

5.5.7 The design bending load for side frame or web frame primary member is to be taken as:

H fr S fr P SS for frames attached to side shell

H fr S fr P LB for frames attached to longitudinal bulkheads.

5.5.8 The membrane loads acting on the side shell or longitudinal bulkhead plating are defined in Vol 1, Pt 7, Ch 2, 4.2 Side shell structures (SS) or Vol 1, Pt 7, Ch 2, 4.5 Longitudinal bulkhead structures (LB). These membrane loads are required to assess the frames in addition to the local bending loads.

5.6 Deck beams (BM)

5.6.1 This sub-Section covers deck beams and deep transverse beams supporting deck structure.

5.6.2 The design normal pressure, P BM, for the web plating of deck beams may be ignored.

5.6.3 The design impulse pressure, P BM, for the web plating of deck beams may be ignored, unless these members are subjected to sloshing loads or similar.

5.6.4 The design vertical load, LV BM, for the deck beam may be ignored.

5.6.5 The design transverse load, LT BM, for the deck beam due to hydrostatic and hydrodynamic compressive loading is to be taken as follows:

LT BM = – P SS H d S bm kN

where

P SS and H d are to be taken as the values defined for the deck plating in Vol 1, Pt 7, Ch 2, 4.3 Strength deck and internal deck structures (DK) 4.3.6

5.6.6 The design shear force, QVBM, for the deck beam web plating is to be based on the pressure loads acting on the plating of the deck P CD (downwards), the local inertial forces [F CD] and pillar bulkhead loads above L A. The shear force acts in the vertical direction and is to be taken as:

QVBM = (B bm S bm P CD + [F CD] + L A )/2 kN

where

S bm = mean spacing of deck beams, in metres, see Figure 2.5.5 Loads to be applied to deck beams
B bm = span of the deck beams between longitudinal bulkheads, pillars or side shell, in metres
L A = load, in kN, from pillar(s) or bulkhead(s) above, assumed zero if there is none over, see Vol 1, Pt 7, Ch 2, 4.2 Side shell structures (SS) 4.2.5
F CD = inertial load or loads, in kN, from items of equipment, etc. on the supported deck, assumed zero if there is none over. F CD is defined in Vol 1, Pt 7, Ch 2, 5.1 Deck structures (DK) 5.1.5

P CD is defined in Vol 1, Pt 7, Ch 2, 5.1 Deck structures (DK) 5.1.2

5.6.7 The design bending load for deck beam primary member is to be taken as:

  1. (B bm S bm P CD + [F CD] + L A) kN

5.6.8 The membrane loads acting on the deck plating are defined in Vol 1, Pt 7, Ch 2, 4.3 Strength deck and internal deck structures (DK) These membrane loads are required to assess the frames in addition to the local bending loads.

Figure 2.5.5 Loads to be applied to deck beams

5.7 Pillars (PI)

5.7.1 The design load, , supported by the pillar is to be taken as:

= –(S pi B pi P CD + L A + [F CD]) kN

where

P CD = inertial deck design pressure, as appropriate, plus any other local loadings directly above the pillar, in kN/m2. Where the pillar supports a deck area over which the design pressure varies, then the summation of the these loads is to be used, see Vol 1, Pt 7, Ch 2, 5.1 Deck structures (DK) 5.1.2
[F CD] = appropriate portion of the inertial load or loads, in kN, from items of equipment, etc. on the supported deck, assumed zero if there is none over. F CD is defined in Vol 1, Pt 7, Ch 2, 5.1 Deck structures (DK) 5.1.5

B pi S pi is the effective deck area supported by the pillar bulkhead

B pi = mean spacing of transverses supported by pillars or transverse bulkheads, in metres, see Figure 2.5.6 Loads supported by a pillar
S pi = mean spacing of girders supported by the pillars, longitudinal bulkheads or side shell, in metres
L A = load, in kN, from pillar(s) or bulkhead(s) above, assumed zero if there is none over may be taken as for the supported pillar or LV PB for the supported bulkhead, see Vol 1, Pt 7, Ch 2, 5.8 Pillar bulkheads (PB)

is not to be taken less than 5 kN.

5.7.2 When any of the conditions below are satisfied then the pillar load should be derived using direct calculation methods:

  • where the structural arrangement is complex;
  • where it is considered that the load in the pillar will not be accurately represented by the above formulae, e.g. pillars supporting decks in way of the ends of a long superstructure block;
  • where the pillar is not supported underneath by the double bottom or substantial structural members.

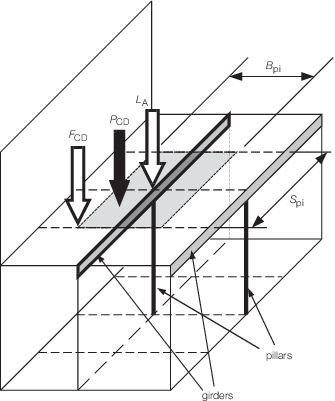
Figure 2.5.6 Loads supported by a pillar

5.8 Pillar bulkheads (PB)

5.8.1 The vertical in-plane compressive load supported by a pillar bulkhead is to be taken as:

LV PB = – (S pb B pb P CD + L A + [F CD]) kN

where

P CD = inertial deck design pressure, as appropriate, plus any other local loadings directly above the pillar, in kN/m2, see Vol 1, Pt 7, Ch 2, 5.1 Deck structures (DK) 5.1.2
[F CD] = inertial load or loads, in kN, from items of equipment, etc. on the supported deck, assumed zero if there is none over. F CD is defined in Vol 1, Pt 7, Ch 2, 5.1 Deck structures (DK) 5.1.5
L A = appropriate portion of the load or loads, in kN, from pillar(s) or bulkhead(s) above, assumed zero if there is none over, may be taken as for the supported pillar or LV PB for the supported bulkhead

S pb, B pb is the effective deck area supported by the pillar bulkhead and can be taken as follows:

  1. For longitudinal pillar bulkheads, see Figure 2.5.7 Loads supported by a pillar bulkhead:

    B pb = mean spacing of longitudinal bulkheads, side shell or effectively supported longitudinal girders, in metres
    S pb = length of the pillar bulkhead between major transverse bulkheads or effectively supported transverse web frames or similar, in metres

  2. For transverse pillar bulkheads:

    S pb = mean spacing of transverse bulkheads or effectively supported transverse web frames or similar, in metres
    B pb = breadth of the pillar bulkhead between major longitudinal bulkheads or the side shell, in metres.

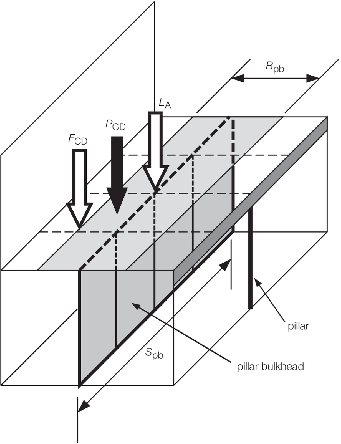
Figure 2.5.7 Loads supported by a pillar bulkhead

5.8.2 When any of the conditions below are satisfied then the pillar bulkhead load should be derived using direct calculation methods:

  • where the structural arrangement is complex;
  • where it is considered that the load in the pillar bulkhead will not be accurately represented by the above formulae, e.g. pillar bulkheads supporting decks in way of the ends of a long superstructure block;
  • where the pillar bulkhead is not supported underneath by the double bottom or substantial structural members.
Copyright 2022 Clasifications Register Group Limited, International Maritime Organization, International Labour Organization or Maritime and Coastguard Agency. All rights reserved. Clasifications Register Group Limited, its affiliates and subsidiaries and their respective officers, employees or agents are, individually and collectively, referred to in this clause as 'Clasifications Register'. Clasifications Register assumes no responsibility and shall not be liable to any person for any loss, damage or expense caused by reliance on the information or advice in this document or howsoever provided, unless that person has signed a contract with the relevant Clasifications Register entity for the provision of this information or advice and in that case any responsibility or liability is exclusively on the terms and conditions set out in that contract.