Section 3 Stress analysis model
Clasification Society 2024 - Version 9.40
Clasifications Register Rules and Regulations - Rules and Regulations for the Classification of Naval Ships, January 2023 - Volume 1 Ship Structures - Part 7 Enhanced Structural Assessment (Provisional) - Chapter 3 Total Load Assessment, TLA - Section 3 Stress analysis model

Section 3 Stress analysis model

Parent topic: Chapter 3 Total Load Assessment, TLA

3.1 General

3.1.1 The stress analysis model given in this Section is to be applied to the total design loads determined in accordance with Vol 1, Pt 7, Ch 2 Total Design Loads.

3.1.2 The stresses, deflections and other values are to be determined for all load cases and all the design load combinations specified in Vol 1, Pt 7, Ch 2, 3 Design load combinations

3.2 Stress determination in primary members

3.2.1 Primary members are major structural members and provide support to decks, major equipment, etc. and also control the cross-sectional and longitudinal shape between decks, side shell and bulkheads. The major primary members are listed in the paragraphs below.

3.2.2 The following structural items are classed as longitudinal primary members:

  • Double bottom girders with attached bottom shell and inner bottom plating.
  • Single bottom girders with attached bottom shell plating.
  • Deck girders.
  • Longitudinal stringers with attached side shell or longitudinal bulkhead plating.
  • Horizontal diaphragms with attached side shell and inner skin plating.

3.2.3 The following structural items are classed as vertical primary members:

  • Deep web frames supporting the side shell or bulkheads including attached plating.
  • Double skin web frames including the attached side shell and inner skin plating.
  • Deep vertical bulkhead stiffeners.

3.2.4 The following structural items are classed as transverse primary members:

  • Double bottom floors with bottom shell and inner bottom plating.
  • Single bottom floors with bottom shell plating.
  • Deep deck or transverse beams with attached deck plating.
  • Double skin deck beam with attached upper and lower deck plating.
  • Transverse bulkhead stringers with attached bulkhead plating.

3.2.5 Primary members support the secondary members and can be considered to act independently of the secondary members. They need to be considered as a large beam supporting local loads with the global and local membrane stresses in the attached plating.

3.2.6 A typical primary member will consist of:

  • Primary attached plating, e.g. bottom shell providing local bending capability.
  • Web plate, providing shear capability.
  • Upper flange or plating for double skin construction providing local bending capability.

The stresses in the attached plating and flange are to be derived in accordance with the requirements of this Section. The stresses in the web plating are to be determined in accordance with Vol 1, Pt 7, Ch 3, 3.3 Stress determination in primary/secondary systems, or Vol 1, Pt 7, Ch 3, 3.4 Stress determination in grillage systems if it is of grillage construction.

3.2.7 The stresses in primary members are to be derived using the recommended equations and stiffener end conditions given in Table 3.3.1 Stress determination in primary members The stress components used in deriving the primary member stresses are given below.

Table 3.3.1 Stress determination in primary members

Stress direction Stress equation Stiffener end condition Notes
Longitudinal primary members
σx σx = σhg + σxb N/mm2 Built in Applicable to the flange and the attached plating
σy σy = σyg N/mm2 (attached to deck plating)
σy = σxv N/mm2 (attached to side shell or long bhd plating) 		N.A. Only applicable to the attached plating
τxy τxy is to be taken as the shear stress for the attached plating, see Vol 1, Pt 7, Ch 3, 3.3 Stress determination in primary/secondary systems or Vol 1, Pt 7, Ch 3, 3.4 Stress determination in grillage systems — Only applicable to the attached plating
Transverse primary members
σx σx = σyg + σxb N/mm2 Built in Applicable to the flange and the attached plating
σy σy = σhg N/mm2 (attached to deck plating)
σy = σxv N/mm2 (attached to transverse bulkhead plating 		N.A. Only applicable to the attached plating
τxy τxy is to be taken as the shear stress for the attached plating, see Vol 1, Pt 7, Ch 3, 3.3 Stress determination in primary/secondary systems or Vol 1, Pt 7, Ch 3, 3.4 Stress determination in grillage systems — Only applicable to the attached plating
Vertical primary members
σx σx = σxv + σxb N/mm2 Built in Applicable to the flange and the attached plating
σy σy = σhg N/mm2 (attached to side shell or long bhd plating)
σy = σyg N/mm2 (attached to transverse bulkhead plating) 		N.A. Only applicable to the attached plating
τxy τxy is to be taken as the shear stress for the attached plating, see Vol 1, Pt 7, Ch 3, 3.3 Stress determination in primary/secondary systems or Vol 1, Pt 7, Ch 3, 3.4 Stress determination in grillage systems — Only applicable to the attached plating
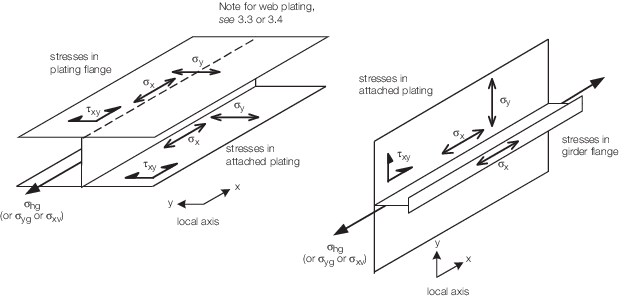
Symbols
σx is along the span of the primary member σhg, σyg and σxv are given in Vol 1, Pt 7, Ch 3, 3.2 Stress determination in primary members 3.2.10
σy is in the normal direction to the span in the attached plating σxb is given in Vol 1, Pt 7, Ch 3, 3.2 Stress determination in primary members 3.2.12
τxy is only applicable to the attached plating      

3.2.8 When it is considered that a different combination of stresses is likely to produce higher stresses, then this combination should be considered.

3.2.9 In general, a primary member will be subject to the following loads:

  • In-plane or axial loading as a consequence hull girder loads, transverse loading due to side shell pressure loads or vertical support loads.
  • Bending loads due to the member supporting out of plane external and internal pressures and equipment or cargo loadings.

3.2.10 The in-plane or axial loading in the primary member attached plating and flanges is to be taken as the membrane stress derived in accordance with the following:

  1. For longitudinally effective primary members:

    σhg is the longitudinal stress due to hull girder bending

  2. For primary members in the transverse direction:

    σyg is the membrane stress due to a global load of LT

  3. For primary members in the vertical direction:

    σxv is the membrane stress due to a vertical load of LV

where

M D = design hull girder bending moment given in Vol 1, Pt 7, Ch 2, 3 Design load combinations
z na = vertical distance above the neutral axis of the structural member under consideration, in metres
hg = the section inertia at the longitudinal position under consideration, see Vol 1, Pt 6, Ch 4, 2.3 Shear strength, in m4
A = is the total area, in cm2, of the primary member including the full breadth of attached plating

LT and LV are defined in Vol 1, Pt 7, Ch 2, 2.1 Nomenclature 2.1.1.

3.2.11 The out of plane bending loads to be applied to the primary member are specified in Vol 1, Pt 7, Ch 2 Total Design Loads. For example, the out of plane bending load for a double bottom girder is specified in Vol 1, Pt 7, Ch 2, 4.6 Bottom longitudinal girders (BG) 4.6.7. In this case the pressure components are to be uniformly distributed over the double bottom girder beam with the point loads applied as individual forces.

3.2.12 The stresses in the flange and attached plating due to bending of the primary member are to be derived as follows:

σxb = is the stress in the plating due to bending of the primary member beam/plate combination under lateral pressure loading or lateral inertial loads
σxb = is to be taken as the negative value of σsp, i.e. σsp,c, when the primary member axial stress is negative, similarly the positive value of σsp, i.e. σsp,t, is to be taken when is the axial stress positive
When appropriate the σxb value is to be the summation of stresses as result of inertial pressures and inertial point loads
σsp,c and σsp,t = are the maximum compressive and tensile stresses in the attached plating of the primary member and are to be derived using the bending stress equations in Vol 1, Pt 7, Ch 3, 2.3 Stresses in secondary and primary member stiffeners 2.3.3, see also Vol 1, Pt 7, Ch 3, 2.3 Stresses in secondary and primary member stiffeners 2.3.6

3.2.13 The section modulus of the primary member with regard to local bending properties is to be derived in accordance with Vol 1, Pt 6, Ch 2, 2.3 Section properties with effective breadths of attached plating as given by Vol 1, Pt 6, Ch 2, 2.2 Effective width of attached plating, be.

3.2.14 The total equivalent stress or von Mises stress, σvm, is to be derived using the following formula:

3.3 Stress determination in primary/secondary systems

3.3.1 The primary members support the secondary members. The secondary stiffeners transfer the lateral loads into the primary members.

3.3.2 An example of a primary/secondary plating and stiffener system is as follows: a longitudinal spacing of 600 mm and a transverse spacing of 2000 mm with the transverse stiffeners having a section inertia value of five times the secondary longitudinal stiffeners.

3.3.3 In a primary/secondary system it is normally sufficient to consider the secondary stiffeners as acting independently of the primary stiffeners. Hence the total stress analysis can ignore the effects of bending of the primary members.

3.3.4 The total stress analysis can be based on the plating between the primary transverse members and need only consider plating membrane stresses and bending stresses in secondary members.

3.3.5 The stresses in the plating of a primary/secondary plating system are to be derived using the recommended equations and stiffener end conditions given in Table 3.3.2 Stress determination in longitudinal plating of primary/secondary systems, e.g., decks and longitudinal bulkheads and Table 3.3.3 Stress determination in transverse plating of primary/secondary systems, e.g., transverse bulkheads The stresses in the flanges of panel stiffeners are given in Vol 1, Pt 7, Ch 3, 2.3 Stresses in secondary and primary member stiffeners 2.3.6 using the conditions given in Vol 1, Pt 7, Ch 3, 3.2 Stress determination in primary members 3.2.3 and Vol 1, Pt 7, Ch 3, 3.3 Stress determination in primary/secondary systems 3.3.3 The stresses and nomenclature are shown in Figure 3.3.1 Definition of stresses in a primary/secondary stiffened panel

Table 3.3.2 Stress determination in longitudinal plating of primary/secondary systems, e.g., decks and longitudinal bulkheads

Stress direction  Stress equation Stiffener end condition
Plating Stiffener flange
Method AA Longitudinal secondary stiffeners
σx Equation A
σx = σxg + σxb N/mm2  		σsx, see Vol 1, Pt 7, Ch 3, 3.11 Derivation of total stresses in stiffener flanges Built in
σy Equation D
σy = σyg N/mm2 		N.A. N.A.
τxy Equation E

δs, see Vol 1, Pt 7, Ch 3, 2.3 Stresses in secondary and primary member stiffeners 2.3.4
τs, see Vol 1, Pt 7, Ch 3, 2.3 Stresses in secondary and primary member stiffeners 2.3.5 		 
Method BB Longitudinal secondary stiffeners adjacent to bulkhead
σx Equation A
σx = σxg + σxb N/mm2  		  Edge end built in. Other end free to deflect,no rotation, see Note 2
σy Equation D
σy = σyg N/mm2 		N.A. N.A.
τxy Equation E

δs, see Vol 1, Pt 7, Ch 3, 2.3 Stresses in secondary and primary member stiffeners 2.3.4
τs, see Vol 1, Pt 7, Ch 3, 2.3 Stresses in secondary and primary member stiffeners 2.3.5 		 
Method CC Transverse secondary stiffeners
σx Equation B
σx = σxg N/mm2 		N.A. N.A.
σy Equation C
σy = σyg + σybN/mm2 		σsx, see Vol 1, Pt 7, Ch 3, 3.11 Derivation of total stresses in stiffener flanges Built in
τxy Equation E

δs, see Vol 1, Pt 7, Ch 3, 2.3 Stresses in secondary and primary member stiffeners 2.3.4
τs, see Vol 1, Pt 7, Ch 3, 2.3 Stresses in secondary and primary member stiffeners 2.3.5 		 

Note 1. The parameters for Equations A to E are given in Vol 1, Pt 7, Ch 3, 3.5 Derivation of the combined longitudinal stress on panels subjected to hull girder bending

Note 2. Alternatively the deflection from the transverse member over its full span, excluding the support from longitudinal stiffeners, may be applied.

Table 3.3.3 Stress determination in transverse plating of primary/secondary systems, e.g., transverse bulkheads

Stress direction  Stress equation Stiffener end condition
Plating Stiffener flange
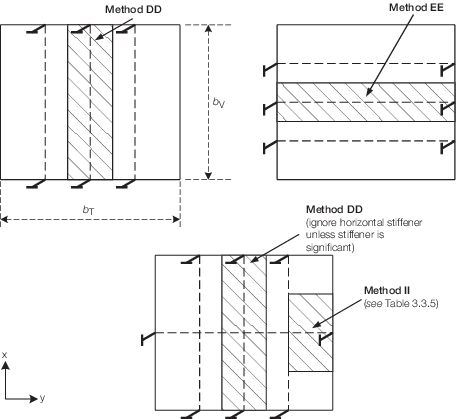
Method DD Vertical secondary stiffeners
σx Equation H
σx = σxg + σxb N/mm2  		σsx, see Vol 1, Pt 7, Ch 3, 3.11 Derivation of total stresses in stiffener flanges N.A.
σy Equation G
σy = σyg N/mm2 		N.A. Built in
τxy Equation J

δs, see Vol 1, Pt 7, Ch 3, 2.3 Stresses in secondary and primary member stiffeners 2.3.4
τs, see Vol 1, Pt 7, Ch 3, 2.3 Stresses in secondary and primary member stiffeners 2.3.5 		 
Method EE Horizontal secondary stiffeners
σx Equation I
σx = σxv N/mm2  		N.A. N.A.
σy Equation F
σy = σyg + σyb N/mm2 		σsx, see Vol 1, Pt 7, Ch 3, 3.11 Derivation of total stresses in stiffener flanges Built in
τxy Equation J

δs, see Vol 1, Pt 7, Ch 3, 2.3 Stresses in secondary and primary member stiffeners 2.3.4
τs, see Vol 1, Pt 7, Ch 3, 2.3 Stresses in secondary and primary member stiffeners 2.3.5 		 

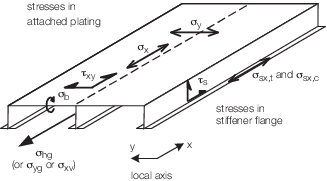
Note The parameters for Equations F to J are given in Vol 1, Pt 7, Ch 3, 3.8 Derivation of the combined transverse stress acting on transversely orientated panels to Vol 1, Pt 7, Ch 3, 3.10 Derivation of the total shear stress on transversely orientated panels.

Figure 3.3.1 Definition of stresses in a primary/secondary stiffened panel

3.3.6 When it is considered that a different combination of stresses is likely to produce higher stresses, then this combination should be considered.

3.3.7 Buckling of plating is to be assessed using the in-plane membrane stresses only. The membrane stresses are to be derived as follows:

  σx using Equation B
  σy using Equation D
  τxy using Equation E

where

Equations B, D and E are defined in Table 3.3.2 Stress determination in longitudinal plating of primary/secondary systems, e.g., decks and longitudinal bulkheads.

3.4 Stress determination in grillage systems

3.4.1 A grillage system of plating and stiffeners is one where the bending stiffness of the orthogonal stiffeners are similar in magnitude and the orthogonal stiffeners work together to support the applied loads. The grillage system is in turn supported by primary structural items such as deep girders, deep transverse beams or bulkheads.

3.4.2 An example of a grillage system is as follows: plating supported by a longitudinal spacing of 600 mm and a transverse spacing of 1500 mm with the transverse stiffeners having an section inertia value of 1,5 times the longitudinal stiffeners.

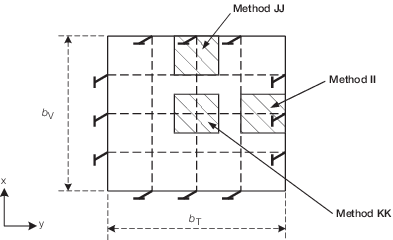
3.4.3 Normally it is necessary to use direct calculations to evaluate the stresses within a grillage plating system. However, it may be sufficient to consider the stiffeners perpendicular to an edge of the grillage panel as acting independently of the grillage system. See Table 3.3.4 Stress determination in longitudinal plating of grillage systems, e.g., decks and longitudinal bulkheads and Methods FF and GG in the attached figure, also Methods II and JJ in Table 3.3.5 Stress determination in transverse plating of grillage systems, e.g., transverse bulkheads..

Table 3.3.4 Stress determination in longitudinal plating of grillage systems, e.g., decks and longitudinal bulkheads

Stress direction  Stress equation Stiffener end condition
Plating Stiffener flange
Method FF At the fore and aft edges of a grillage panel
σx Equation A
σx = σxg + σxb N/mm2  		σsx, see Vol 1, Pt 7, Ch 3, 3.1 General 3.1.1 Edge end built in. Other end free to deflect, no rotation, see Note 2
σy Equation D
σy = σyg N/mm2 		N.A. N.A.
τxy Equation E

δs, see Vol 1, Pt 7, Ch 3, 2.3 Stresses in secondary and primary member stiffeners 2.3.4
τs, see Vol 1, Pt 7, Ch 3, 2.3 Stresses in secondary and primary member stiffeners 2.3.5 		 
Method GG At the port and starboard edges of a grillage panel
σx Equation B
σx = σxg N/mm2  		N.A. N.A.
σy Equation C
σy = σyg + σyb N/mm2 		σsx, see Vol 1, Pt 7, Ch 3, 3.11 Derivation of total stresses in stiffener flanges Edge end built in. Other end free to deflect, no rotation, see Note 3
τxy Equation E

δs, see Vol 1, Pt 7, Ch 3, 2.3 Stresses in secondary and primary member stiffeners 2.3.4
τs, see Vol 1, Pt 7, Ch 3, 2.3 Stresses in secondary and primary member stiffeners 2.3.5 		 
Method HH At the centre of a grillage panel
σx Equation A
σx = σxg + σxb N/mm2  		σsx, see Vol 1, Pt 7, Ch 3, 3.11 Derivation of total stresses in stiffener flanges Built in
σy Equation C
σy = σyg + σybN/mm2 		σsx, see Vol 1, Pt 7, Ch 3, 3.11 Derivation of total stresses in stiffener flanges Built in
τxy Equation E

δs, see Vol 1, Pt 7, Ch 3, 2.3 Stresses in secondary and primary member stiffeners 2.3.4
τs, see Vol 1, Pt 7, Ch 3, 2.3 Stresses in secondary and primary member stiffeners 2.3.5 		 

Note 1. The parameters for Equations A to E are given in Vol 1, Pt 7, Ch 3, 3.5 Derivation of the combined longitudinal stress on panels subjected to hull girder bending to Vol 1, Pt 7, Ch 3, 3.7 Derivation of the total shear stress.

Note 2. Alternatively the deflection from the longitudinal member over its full span, excluding the support from transverse stiffeners, may be applied.

Note 3. Alternatively the deflection from the transverse member over its full span, excluding the support from longitudinal stiffeners, may be applied.

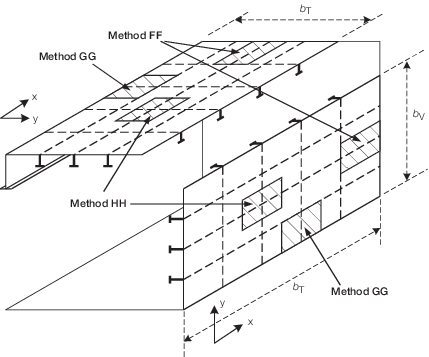
Table 3.3.5 Stress determination in transverse plating of grillage systems, e.g., transverse bulkheads.

Stress direction  Stress equation Stiffener end condition
Plating Stiffener flange
Method II Horizontal stiffeners at the port and starboard edges of a grillage panel
σx Equation I
σx = σxv N/mm2  		N.A. Edge end Built in.
Other end free to deflect, no rotation, see Note 2
σy Equation F
σy = σyg + σyb N/mm2 		σsx, see Vol 1, Pt 7, Ch 3, 3.11 Derivation of total stresses in stiffener flanges N.A.
τxy Equation J

δs, see Vol 1, Pt 7, Ch 3, 2.3 Stresses in secondary and primary member stiffeners 2.3.4
τs, see Vol 1, Pt 7, Ch 3, 2.3 Stresses in secondary and primary member stiffeners 2.3.5 		—
Method JJ Vertical stiffeners at the top and bottom edges of a grillage panel
σx Equation H
σx = σxv + σxb N/mm2  		σsx, see Vol 1, Pt 7, Ch 3, 3.11 Derivation of total stresses in stiffener flanges N.A.
σy Equation G
σy = σyg N/mm2 		N.A. Edge end built in. Other end free to deflect, no rotation, see Note 3
τxy Equation J

δs, see Vol 1, Pt 7, Ch 3, 2.3 Stresses in secondary and primary member stiffeners 2.3.4
τs see Vol 1, Pt 7, Ch 3, 2.3 Stresses in secondary and primary member stiffeners 2.3.5 		—
Method KK At the centre of a grillage panel
σx Equation H
σx = σxv + σxb N/mm2  		σsx, see Vol 1, Pt 7, Ch 3, 3.11 Derivation of total stresses in stiffener flanges Built in
σy Equation F
σy = σyg + σyf + σyb N/mm2 		σsx, see Vol 1, Pt 7, Ch 3, 3.11 Derivation of total stresses in stiffener flanges Built in
τxy Equation J

δs, see Vol 1, Pt 7, Ch 3, 2.3 Stresses in secondary and primary member stiffeners 2.3.4
τs, see Vol 1, Pt 7, Ch 3, 2.3 Stresses in secondary and primary member stiffeners 2.3.5 		—

Note 1. The parameters for Equations F to J are given in Vol 1, Pt 7, Ch 3, 3.8 Derivation of the combined transverse stress acting on transversely orientated panels to Vol 1, Pt 7, Ch 3, 3.10 Derivation of the total shear stress on transversely orientated panels.

Note 2. Alternatively the deflection of the vertical member over its full span, excluding the support from horizontal stiffeners, may be applied instead of the free to deflect condition.

Note 3. Alternatively the deflection from the horizontal member over its full span, excluding the support from vertical stiffeners, may be applied instead of the free to deflect condition.

3.4.4 The bending stresses in the edge stiffeners may be evaluated on the basis of encastre at the edge of the grillage panel and no rotation and free to deflect at the intersection with the first orthogonal stiffener.

3.4.5 In this case, the total stress analysis is to be based on the membrane stress in the plating of the grillage panel and consider the bending stresses in the middle stiffener perpendicular to the edge of the panel.

3.4.6 It will be necessary to derive the total stress at the edge of the panel for each stiffener direction.

3.4.7 The total stress in the centre of the grillage panel should also be checked. In this case it is necessary to consider the stresses in the plate due to bending of the stiffener in each direction as well as the plating stresses due to membrane loads.

3.4.8 The stresses in the plating of a grillage plating system are to be derived using the recommended equations and stiffener end conditions given in Table 3.3.4 Stress determination in longitudinal plating of grillage systems, e.g., decks and longitudinal bulkheads and Vol 1, Pt 7, Ch 3, 3.3 Stress determination in primary/secondary systems 3.3.5 The stresses in the flanges of the panel stiffener are given by Vol 1, Pt 7, Ch 3, 2.3 Stresses in secondary and primary member stiffeners 2.3.6, using the conditions given in Table 3.3.4 Stress determination in longitudinal plating of grillage systems, e.g., decks and longitudinal bulkheads and Table 3.3.5 Stress determination in transverse plating of grillage systems, e.g., transverse bulkheads.. The stresses are illustrated in Figure 3.3.2 Definition of stresses in a grillage stiffened panel

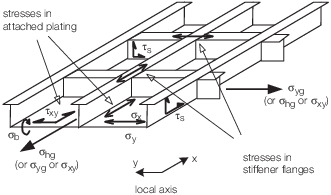
Figure 3.3.2 Definition of stresses in a grillage stiffened panel

3.4.9 When it is considered that a different combination of stresses is likely to produce higher stresses, then this combination should be considered.

3.4.10 Buckling of plating is to be assessed using the in-plane membrane stresses only. The membrane stresses are to be derived as follows:

  σx using Equation B
  σy using Equation D
  τxy using Equation E

where

Equations B, D and E are defined in Table 3.3.4 Stress determination in longitudinal plating of grillage systems, e.g., decks and longitudinal bulkheads

3.5 Derivation of the combined longitudinal stress on panels subjected to hull girder bending

3.5.1 The longitudinal stresses in the plating and stiffener flanges for structural members subjected to hull girder bending loads as well as lateral loads are to be derived using the equations specified in this Section, see Table 3.3.2 Stress determination in longitudinal plating of primary/secondary systems, e.g., decks and longitudinal bulkheads and Table 3.3.4 Stress determination in longitudinal plating of grillage systems, e.g., decks and longitudinal bulkheads

3.5.2  Equation A is used for grillage systems or plating systems with the secondary stiffeners orientated in the longitudinal direction. For these systems, the stress in the plating/stiffener combination due to local bending needs to be considered in addition to the membrane stresses due to hull girder bending. The stress components in Equation A are given below.

3.5.3  Equation B is used for plating systems with the secondary stiffeners orientated in the transverse (or vertical) direction. For these systems only the longitudinal stress due to hull girder bending needs to be considered.

3.5.4 The longitudinal stress components associated with Equations A and B are given below:

σxg = is the longitudinal membrane stress due to hull girder bending
σxb = is the stress in the plating due to bending of the longitudinal stiffener/plate combination under lateral pressure loading or lateral inertial loads
Normally σxb is to be taken as the negative value of σsp, i.e. σsp,c, when the hull girder bending stress σxg is negative, similarly the positive value of σsp, i.e. σsp,t, is to be taken when σxg is positive, see Figure 3.2.2 Bending stresses in stiffener beam However, there may be cases where it is necessary to consider the opposite situation
When appropriate, the σxb value is to be the summation of stresses as result of inertial pressures and inertial point loads
σsp,c and σsp,t = are the maximum compressive and tensile stresses in the plating of the stiffener/plate combination and are to be derived using the bending stress equations in Vol 1, Pt 7, Ch 3, 2.3 Stresses in secondary and primary member stiffeners 2.3.3, see also Vol 1, Pt 7, Ch 3, 2.3 Stresses in secondary and primary member stiffeners 2.3.6
M D = design hull girder bending moment, in kNm given in Vol 1, Pt 7, Ch 2, 3 Design load combinations
z na = vertical distance above the neutral axis of the structural member under consideration, in metres
hg = the section inertia at the longitudinal position under consideration, see Vol 1, Pt 6, Ch 4, 2 Hull girder strength, in m4.

3.6 Derivation of the combined transverse stress acting on panels subjected to hull girder bending

3.6.1 The transverse stresses in the plating and stiffener flanges for structural members subjected to transverse loads as well as lateral loads are to be derived using the equations specified in this Section, see Table 3.3.2 Stress determination in longitudinal plating of primary/secondary systems, e.g., decks and longitudinal bulkheads and Table 3.3.4 Stress determination in longitudinal plating of grillage systems, e.g., decks and longitudinal bulkheads

3.6.2  Equation C is used for grillage systems or plating systems with the secondary stiffeners orientated in the transverse direction. For these systems, the stress in the plating/stiffener combination due to local bending needs to be considered in addition to membrane stresses due to global transverse loading. The stress components in Equation C are given below.

3.6.3  Equation D is used for plating systems with the secondary stiffeners orientated in the longitudinal direction. For these systems, only membrane stress due to global transverse loading needs to be considered.

3.6.4 The transverse stress components associated with equations C and D are given below:

σyg = is the membrane stress due to global transverse loading
σyb = is the stress in the plating due to bending of the longitudinal stiffener/plate combination under lateral pressure loading or lateral inertial loads
Normally, σyb is to be taken as the negative value of σsp, i.e. σsp,c, when the global transverse stress σyg is negative, similarly the positive value of σsp, i.e. σsp,t, is to be taken when σyg is positive, see Figure 3.3.2 Definition of stresses in a grillage stiffened panel. However, there may be cases where it is necessary to consider the opposite situation.
When appropriate, the σyb value is to be the summation of stresses as result of inertial pressures and inertial point loads
σsp,c and σsp,t = are the maximum compressive and tensile stresses in the plating of the stiffener/plate combination and are to be derived using the bending stress equations in Vol 1, Pt 7, Ch 3, 2.3 Stresses in secondary and primary member stiffeners 2.3.3, see also Vol 1, Pt 7, Ch 3, 2.3 Stresses in secondary and primary member stiffeners 2.3.6
LT = is the appropriate transverse design load, in kN, given in Vol 1, Pt 7, Ch 2 Total Design Loads, i.e. LT DK, LT BS, etc.
t p = thickness of plating, in mm
b L = breadth of plating, in metres, over which the load LT applies. Normally, this is the distance between decks or the height of the plating panel.

3.7 Derivation of the total shear stress

3.7.1  Equation E is used to derive the total shear stress in the plating for all plating systems.

3.7.2 The shear stress components associated with Equation E are given below:

|Q| = denotes the absolute value of parameter Q
hg =
Q D = is global hull girder shear force, in kN. This will be zero for all transverse plating systems
Q T = local shear force due to local transverse loads, in kN, given in Vol 1, Pt 7, Ch 2 Total Design Loads, e.g. QT DK, QT ST
QV = local shear force due to local inertial forces, in kN, given in Vol 1, Pt 7, Ch 2 Total Design Loads, e.g. QV DG, QV BG

A z, hg and δi are given in Vol 1, Pt 6, Ch 4, 2.3 Shear strength 2.3.6

NOTE

All shear force loads are to be assumed positive.

3.8 Derivation of the combined transverse stress acting on transversely orientated panels

3.8.1 The transverse stresses in the plating and stiffener flanges for structural members subjected to transverse loads as well as lateral loads are to be derived using the equations specified in this Section, see Table 3.3.3 Stress determination in transverse plating of primary/secondary systems, e.g., transverse bulkheads and Table 3.3.5 Stress determination in transverse plating of grillage systems, e.g., transverse bulkheads.

3.8.2  Equation F is used for grillage systems or plating systems with the secondary stiffeners orientated in the transverse direction.

3.8.3  Equation G is used for plating systems with the secondary stiffeners orientated in the vertical direction.

3.8.4 The transverse stress components associated with Equations F and G are given in Vol 1, Pt 7, Ch 3, 3.6 Derivation of the combined transverse stress acting on panels subjected to hull girder bending 3.6.4.

3.9 Derivation of the combined vertical stress acting on transversely orientated panels

3.9.1 The vertical stresses in the plating and stiffener flanges for structural members subjected to vertical loads as well as lateral loads are to be derived using the equations specified in this Section, see Table 3.3.3 Stress determination in transverse plating of primary/secondary systems, e.g., transverse bulkheads and Vol 1, Pt 7, Ch 3, 3.3 Stress determination in primary/secondary systems 3.3.5

3.9.2  Equation H is used for grillage systems or plating systems with the transverse secondary stiffeners orientated in the vertical direction.

3.9.3  Equation I is used for plating systems with the secondary stiffeners orientated in the transverse direction.

3.9.4 The vertical stress components associated with Equations H and I are given below:

σxv = is the membrane stress due to vertical loading
= N/mm2
σxb = is the stress in the plating due to bending of the longitudinal stiffener/plate combination under lateral pressure loading or lateral inertial loads
Normally σxb is to be taken as the negative value of σsp, i.e. σsp,c, when the vertical stress σxv is negative, similarly the positive value of σsp, i.e. σsp,t, is to be taken when σxv is positive, see Vol 1, Pt 7, Ch 3, 3.2 Stress determination in primary members 3.2.2. However, there may be cases where it is necessary to consider the opposite situation
When appropriate, the σxb value is to be the summation of stresses as result of inertial pressures and inertial point loads
σsp,c and σsp,t = are the maximum compressive and tensile stresses in the plating of the stiffener/plate combination and are to be derived using the bending stress equations in Vol 1, Pt 7, Ch 3, 2.3 Stresses in secondary and primary member stiffeners 2.3.3, see also Vol 1, Pt 7, Ch 3, 2.3 Stresses in secondary and primary member stiffeners 2.3.6

where

LV = is the design load, in kN, given in Vol 1, Pt 7, Ch 2 Total Design Loads, e.g. LV SS, LV BH
t p = thickness of plating, in mm
b T = breadth of plating, in metres, over which the load LV applies. Normally, this is the distance between the side shell(s) or longitudinal bulkheads but it is to be reduced for the presence of large openings.

3.10 Derivation of the total shear stress on transversely orientated panels

3.10.1  Equation J is used to derive the total shear stress in any plating system which is not subjected to global hull girder shear force.

3.10.2 The shear stress components associated with Equation J are given below:

Q T = local shear force due to local transverse loads, in kN, given in Vol 1, Pt 7, Ch 2 Total Design Loads, e.g. QT DK, QT SF, QT ST
QV = local shear force due to local inertial forces, in kN, given in Vol 1, Pt 7, Ch 2 Total Design Loads, e.g. QV BM, QV DG, QV BG, QV FL

NOTE

All shear force loads are to be assumed positive.

3.11 Derivation of total stresses in stiffener flanges

3.11.1 The total compressive and tensile stresses in stiffener flanges, σsx, are given by the following:

σsx,c = σax + σsf,c N/mm2 (compressive)
σ sx,t = σax + σsf,t N/mm2 (tensile)

where

σax = is the axial stress in the stiffener at the combined stiffener plate neutral axis, this is normally to be taken as the membrane stress in the plating, i.e. σxg, σyg or σxv depending on the orientation of the stiffener, see Vol 1, Pt 7, Ch 3, 3.5 Derivation of the combined longitudinal stress on panels subjected to hull girder bending 3.5.4, Vol 1, Pt 7, Ch 3, 3.6 Derivation of the combined transverse stress acting on panels subjected to hull girder bending 3.6.4 or Vol 1, Pt 7, Ch 3, 3.9 Derivation of the combined vertical stress acting on transversely orientated panels 3.9.4
σsf,t, σsf,c = are the tensile and compressive bending stresses the stiffener flange, see Vol 1, Pt 7, Ch 3, 2.3 Stresses in secondary and primary member stiffeners 2.3.3 and Vol 1, Pt 7, Ch 3, 2.3 Stresses in secondary and primary member stiffeners 2.3.6, using the appropriate boundary conditions given in Vol 1, Pt 7, Ch 3, 3 Stress analysis model

3.11.2 These formulae may be applied to grillage and primary/secondary stiffened plating systems. The stresses in a stiffener beam subjected to more than one load may be derived by adding the stresses from each load component.

3.12 Derivation of total equivalent stress

3.12.1 The total equivalent stress or von Mises stress, σvm, is to be derived using the following formula:

Copyright 2022 Clasifications Register Group Limited, International Maritime Organization, International Labour Organization or Maritime and Coastguard Agency. All rights reserved. Clasifications Register Group Limited, its affiliates and subsidiaries and their respective officers, employees or agents are, individually and collectively, referred to in this clause as 'Clasifications Register'. Clasifications Register assumes no responsibility and shall not be liable to any person for any loss, damage or expense caused by reliance on the information or advice in this document or howsoever provided, unless that person has signed a contract with the relevant Clasifications Register entity for the provision of this information or advice and in that case any responsibility or liability is exclusively on the terms and conditions set out in that contract.